AMC 10A 2020 Problem 6 | Divisibility Problem

Try this beautiful Problem based on Divisibility Problem from AMC 2020 Problem 6.

Divisibility Problem: AMC 10A 2020 Problem 6

How many 4-digit positive integers (that is, integers between 1000 and 9999 , inclusive) having only even digits are divisible by 5 ?

Key Concepts

Divisibility

Counting Principle

Suggested Book | Source | Answer

AMC 10A 2020 Problem 6

100

Try with Hints

What is the divisibility rule for a number divisible by 5?

Now apply this for unit, tens, hundred and thousand digits.

Here the unit digit must be 0. So I just have one choice for units place.

The middle two digits can be 0, 2, 4, 6, or 8.

But the thousands digit can only be 2, 4, 6, or 8 since it cannot be zero.

Now try to count how many choices are there for each position.

Then there was 1 choice for unit digit.

5 choices for middle two digits.

4 choices for thousands digit.

Now calculate the total number of choices you can make.

ISI MStat PSB 2012 Problem 6 | Tossing a biased coin

This is a very beautiful sample problem from ISI MStat PSB 2012 Problem 6 based on Conditional probability . Let's give it a try !!

Problem- ISI MStat PSB 2012 Problem 6

There are two biased coins - one which has probability $1 / 4$ of showing
heads and $3 / 4$ of showing tails, while the other has probability $3 / 4$ of showing heads and $1 / 4$ of showing tails when tossed. One of the two coins is chosen at random and is then tossed 8 times.

(a) Given that the first toss shows heads, what is the probability that in the next 7 tosses there will be exactly 6 heads and 1 tail?
(b) Given that the first toss shows heads and the second toss shows tail, what is the probability that the next 6 tosses all show heads?

Prerequisites

Basic Counting Principle

Solution :

Let , $A_1$: Coin with probability of Head 1/4 and Tail 3/4 is chosen
$A_2$ : Coin with probability of Head 3/4 and Tail 1/4 is chosen
B :first toss shows heads and the next 7 tosses there will be exactly 6 heads and 1 tail .
C : the first toss shows heads and the second toss shows tail and the next 6 tosses all show heads .

(a) $ P(B)=P(B|A_1)P(A_1) + P(B|A_2)P(A_2) $

Now , $ P(B|A_1)= \frac{1}{4} \times {7 \choose 1} \times (\frac{1}{4})^{6} \times \frac{3}{4} $

Since , first toss is head so it can occur by coin 1 with probability 1/4 and out of next 7 tosses we can choose 6 where head comes and this occurs with probability $ {7 \choose 1} \times (\frac{1}{4})^{6} \times \frac{3}{4} $

Similarly we can calculate $ P(B|A_2) $ and $ P(A_1)=P(A_2)= 1/2 $ the probability of choosing any one coin out of 2 .

Therefore , $ P(B)=P(B|A_1)P(A_1) + P(B|A_2)P(A_2) $

= $ \frac{1}{4} \times {7 \choose 1} \times\left(\frac{1}{4}\right)^{6} \times \frac{3}{4} \times\frac{1}{2}+\frac{3}{4} \times {7 \choose 1} \times\left(\frac{3}{4}\right)^{6} \times \frac{1}{4} \times \frac{1}{2} $

(b) Similarly like (a) we get ,

$ P(C)= \frac{1}{4} \times \frac{3}{4} \times (\frac{1}{4})^{6} \times \frac{1}{2}+\frac{3}{4} \times \frac{1}{4} \times\left(\frac{3}{4}\right)^{6} \times \frac{1}{2} $ .

Here we don't need to choose any thing as all the outcomes of the toss are given we just need to see for two different coins .

Food For Thought

There are 10 boxes each containing 6 white and 7 red balls. Two different boxes are chosen at random, one ball is drawn simultaneously at random from each and transferred to the other box. Now a box is again chosen from the 10 boxes and a ball is chosen from it.Find out the probability of the ball being white.

Outstanding Statistics Program with Applications

ISI MStat PSB 2013 Problem 3 | Number of distinct integers

This is a very beautiful sample problem from ISI MStat PSB 2013 Problem 3 based on Counting principle . Let's give it a try !!

Problem- ISI MStat PSB 2013 Problem 3

Suppose integers are formed by taking one or more digits from the
following $ 2,2,3,3,4,5,5,5,6,7 $ . For example, 355 is a possible choice while 44 is not. Find the number of distinct integers that can be formed in which
(a) the digits are non-decreasing;
(b) the digits are strictly increasing.

Prerequisites

Basic Counting Principle

Solution :

(a) To find the number of integers with non-decreasing digits we will go by this way

First see that the position of given digits are fixed as they have to form non-decreasing digits what can be do is to select number of times the particular digit occurs .

For example 223556 in an integer With non-decreasing digits so here 2 occurs
2 times, 3 occurs 1 times, 4 doesn't occurs any times, 5 occurs 2 times, 6 occur 1 time and finally 7 which doesn't occur any number of times.
So, here we have (0,1,2) possible choices of occurrence of 2 ,(0,1,2) possible choices of occurrence of $ 3, \cdots,$ (0,1) possible choices of occurrence of 7 .

Hence, number of such integers $=3 \times 3 \times 2 \times 4 \times 2 \times 2-1$.

We are subtracting 1 to exclude the case where no digits has occur any number of times.

(b) To find the number of integers with increasing digits we can go by above method. Here there is only one restriction that a digit must be greater than it's preceding digits.so, no consecutive digits can be equal. Hence every digits has two choices (0,1) of occurrence . Therefore number of such integers = $ 2^{6}-1$ .

We are subtracting 1 to exclude the case where no digits has occur any number of times.

Food For Thought

A number is chosen randomly from all the 5 digited numbers.Find out the probability that the digits form a non decreasing sequence.

Hint 1 : Find what is invariant here .

Hint 2 : Use the non-negative integer solutions of a equation formula .

Outstanding Statistics Program with Applications

ISI MStat PSB 2013 Problem 9 | Envelope Collector's Expenditure

This is a very simple and beautiful sample problem from ISI MStat PSB 2013 Problem 9. It is mainly based on geometric distribution and its expectation . Try it!

Problem- ISI MStat PSB 2013 Problem 9

Envelopes are on sale for Rs. 30 each. Each envelope contains exactly one coupon, which can be one of the one of four types with equal probability. Suppose you keep on buying envelopes and stop when you collect all the four type of coupons. What will be your expenditure ?

Prerequisites

Geometric Distribution

Expectation of geometric distribution

Basic counting

Solution :

This problem seems quite simple and it is simple, often one may argue that we can take a single random variable, which denotes the number of trials till the fourth success (or is it third !!), and calculate its expectation. But I differ here becaue I find its lot easier to work with sum of geometric random variables than a negative binomial. ( negative binomial is actually sum of finite geometrics !!)

So, here what we will do, is define 4 random variables, as $X_i$ : # trials to get a type of coupon that is different from the all the $(i-1)$ types of coupons drawn earlier. $i=1,2,3,4$.

Now since each type of coupon has an equal probability to come, that is probability of success is $\frac{1}{4}$, here a common mistakes people commit is assuming all $X_1,X_2,X_3,X_4$ are i.i.d Geometric($\frac{1}{4}$), and this turns out to be a disaster !! So, be aware and observe keenly, that at the first draw, any of the four types will come, with probability 1, and there after we just need the rest of the 3 types to appear at least once. So, here $X_1=1$ always and $X_2 \sim Geo(\frac{3}{4})$( becuase since in the first trial, surely any of the four types will come, our success would be getting any of the 3 types of envelopes from the all types making the success probability $\frac{3}{4}$) similarly , $X_3 \sim Geo(\frac{1}{2})$ and $X_4 \sim Geo(\frac{1}{4})$.

Now for the expectated expenditure at the given rate of Rs. 30 per envelope, expected expenditure is Rs.$30 E(X_1+X_2+X_3+X_4)$

Now, we know that $E(X_2)=\frac{4}{3}$, $E(X_3)=2$ and $E(X_4)=4$ (why??)

So, $E(X_1+X_2+X_3+X_4)=1+\frac{4}{3}+2+4=\frac{25}{3}$.

So, our required expectation is Rs. 250. Hence we are done !

Food For Thought

Suppose among the envelopes you collected each envelope has an unique 5 digit number, you picked an envelope randomly and what is the chance of the number that is going to show up is has its digits in a non-decreasing order ?

How does the chances may vary if you find a k digit number on the envelope ? think over it !!

Outstanding Statistics Program with Applications

ISI MStat PSB 2013 Problem 10 | Balls-go-round

This is a very beautiful sample problem from ISI MStat PSB 2013 Problem 10. It's based mainly on counting and following the norms stated in the problem itself. Be careful while thinking !

Problem- ISI MStat PSB 2013 Problem 10

There are 10 empty boxes numbered 1,2,......,10 placed sequentially on a circle as shown in the figure,

We perform 100 independent trials. At each trial one box is selected with probability $\frac{1}{10}$ and a ball is placed in each of the two neighboring boxes of the selected one.

Define $X_k$ be the number of balls in the $k^{th}$ box at the end of 100 trials.

(a) Find $E(X_k)$ for $ 1 \le k \le 10$.

(b) Find $Cov(X_k, X_5)$ for $1 \le k \le 10 $.

Prerequisites

Counting principles

Binomial Distribution

Independence of Events

Solution :

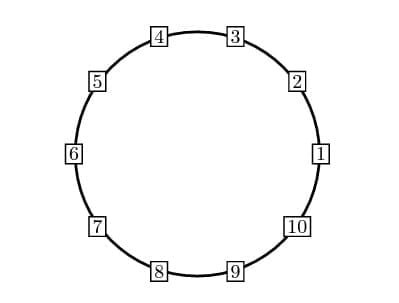
At first this problem may seem a bit of complex, but when one get to see the pattern it starts unfolding. For his types of problem, I find a useful technique is to follow the picture, in this case the picture is being provided, (if not draw it yourself !!)

Given, $X_k$ : # balls in the $k^{th}$ box at the end of 100 trials.

So, the possible values of $X_k$ are 0,1,2,.....,100. and the probability that at the jth trial a ball will added to the kth box is $\frac{1}{10}$ , (why??) .

Now, $P(X_k=x)$= ${100 \choose x}$$ (\frac{1}{5})^{x}$ $ (\frac{4}{5})^{100-x} $ $ x=0,1,......,100$

Clearly, $ X_k \sim binomial( 100, \frac{1}{5})$, from here one can easily find out the the expectation of $X_k$. But have you thought like this ??

Now, notice that after every slelection of box, 2 balls are added in the system, so at the end of the 10th trial, there will be 200 balls distributed in the system.

So, $X_1 +X_2 +.......+ X_{100} =200 $, which implies $ \sum_{k} E(X_k)=200$, due to symmetry $E(X_k)=E(X_l) \forall k \neq l $, So, $E(X_k)=20$.

(b) Now this part is the cream of this problem, first notice that number of balls in kth box, is dependent on the number of balls in the (k-2)th and (k+2)th box, and vice versa, So, $Cov( X_k, X_l)=0$ if $|k-l|\neq 2$.

So, $Cov(X_k, X_5)= 0 \forall k \neq 3,5 \&\ 7 $, so we just need to find the $Cov(X_7,X_5)$ and $Cov(X_3,X_5)$, and $Cov(X_5,X_5)=Var(X_5)$ .

Now it is sufficient to find the covariance of any of the the above mentioned covariances, as both are symmetric and identical to each other. But for the finding say $Cov(X_3,X_5)$, lets look whats happening in each trial more closely,

let, $X_k= i_{k_1} +i_{k_2}+......+i{k_{100}} $ where , $ i_{k_j} = \begin{cases} 1 & if\ a\ ball\ added\ to\ the\ kth\ box\ at\ the\ jth\ trial\ \\ 0 & otherwise \end{cases}$

So, clearly, $P(i_{k_j}=1)=\frac{1}{5} $ ; j=1,2,....,100.

So, $Cov(X_3,X_5)=Cov( i_{3_1}+i_{3_2}+.....+i_{3_{100}},i_{5_1}+i_{5_2}+....+i_{5_{100}})=\sum_{j=1}^{100} Cov(i_{3_j},i_{5_j})$, [$Cov(i_{3_j},i_{5_j*})=0 \forall j\neq j*$, why ?? ].

So, $Cov(X_3,X_5)= 100 Cov(i_{3_1},i_{5_1})=100( E(i_{3_1}i_{5_1})-E(i_{3_1})E(i_{5_1}))=100(P(i_{3_1}=1, i_{5_1}=1)-P(i_{3_1}=1)P(i_{5_1}=1))=100(\frac{1}{10}- \frac{1}{5}\frac{1}{5})=6$.

similarly, $Cov(X_7,X_5)=6$ also, and its easy to find $Var(X_5)$ , so I leave it as an exercise. So, $Cov(X_k,X_5)= \begin{cases} 6 & k=3,7 \\ Var(X_5) & k=5 \\ 0 & k\neq 3,5 \or\ 7\end{cases}$. Hence we are done !!

Food For Thought

Wait, lets imagine, these boxes are interchanged in such a way that the hth box is replaced with the kth ($\neq h$) box, this has been done for all possible pairs of (h,k), Now can you show that all there are precisely $ 10!\sum_{i+2j=10}(i!j!2^j)^{-1}$ number of arrangements possible ?

Now imagine, in a game there are 1 balls each in every box( boxes are arranged identically as shown in the question), you pick up the ball from the first box and put it into the 2nd one, now you can't take out any ball from a box in which you just put a ball, so you pick a ball from the 3rd box and put it into the 4th and you go on like this, taking a ball frim the ith box and put it into the (i+1)th box, but cant empty the box you just filled. Now, again after the first round you remove the empty boxes and do the same thing again and again, till all the balls are not accumulated in a single box. Which box you think will contain all the balls after you run this process finitely many time ?? If you are in this lottery and you are to choose a bix before this game begin, which box you must choose ??

if the coordinator of the game, starts with any ith box how should your strategy change ?? Give it a thought !!

For help, look for Josephus Problem, you may be moved by it's beauty !

Outstanding Statistics Program with Applications

ISI MStat PSA 2019 Problem 6 | Basic Counting principles

This is a beautiful problem from ISI MSTAT 2019 PSA problem 6 based on basic counting principles. We provide sequential hints so that you can try.

Basic Counting Principles - ISI MStat Year 2019 PSA - 6

How many times does the digit ‘2’ appear in the set of integers $ \{1,2,…,1000\} $?

Key Concepts

Basic counting principles

Check the Answer

Answer: is 300

ISI MStat 2019 PSA Problem 6

A First Course in Probability by Sheldon Ross

Try with Hints

Let’s count the number of times 2 occurs once.

_ _ _

The position of 2 can be selected in 3 ways. The rest in 9 x 9.

Total number of 2 = 1 x 3 x 9 x 9 = 243

Let’s count the number of times 2 occurs twice.

_ _ _

The positions of 2 can be selected in 3 ways. The rest in 9.

Total number of 2 = 2 x 3 x 9 = 54

Let’s count the number of times 2 occurs thrice.

The positions of 2 can be selected in 1 way. The rest in 1.

Total number of 2 = 3 x 1 x 1 = 3

Total Number of Such Numbers = 243 + 54 + 3 = 300

Divisibility Problem: AMC 10A 2020 Problem 6

Key Concepts

Suggested Book | Source | Answer

Try with Hints

Other useful links

Related Program

Subscribe to Cheenta at Youtube

Problem- ISI MStat PSB 2012 Problem 6

Prerequisites

Solution :

Food For Thought

Similar Problems and Solutions

Related Program

Outstanding Statistics Program with Applications

Subscribe to Cheenta at Youtube

Problem- ISI MStat PSB 2013 Problem 3

Prerequisites

Solution :

Food For Thought

Similar Problems and Solutions

Related Program

Outstanding Statistics Program with Applications

Subscribe to Cheenta at Youtube

Problem- ISI MStat PSB 2013 Problem 9

Prerequisites

Solution :

Food For Thought

Similar Problems and Solutions

Related Program

Outstanding Statistics Program with Applications

Subscribe to Cheenta at Youtube

Problem- ISI MStat PSB 2013 Problem 10

Prerequisites

Solution :

Food For Thought

Similar Problems and Solutions

Related Program

Outstanding Statistics Program with Applications

Subscribe to Cheenta at Youtube

Basic Counting Principles - ISI MStat Year 2019 PSA - 6

Key Concepts

Check the Answer

Try with Hints

Similar Problems and Solutions

Related Program

Outstanding Statistics Program with Applications

Subscribe to Cheenta at Youtube