Collatz Conjecture and a simple program
Author: Kazi Abu Rousan
Mathematics is not yet ready for such problems.
Paul Erdos
Introduction
A problem in maths which is too tempting and seems very easy but is actually a hidden demon is this Collatz Conjecture. This problems seems so easy that it you will be tempted, but remember it is infamous for eating up your time without giving you anything. This problem is so hard that most mathematicians doesn't want to even try it, but to our surprise it is actually very easy to understand. In this article our main goal is to understand the scheme of this conjecture and how can we write a code to apply this algorithm to any number again and again.
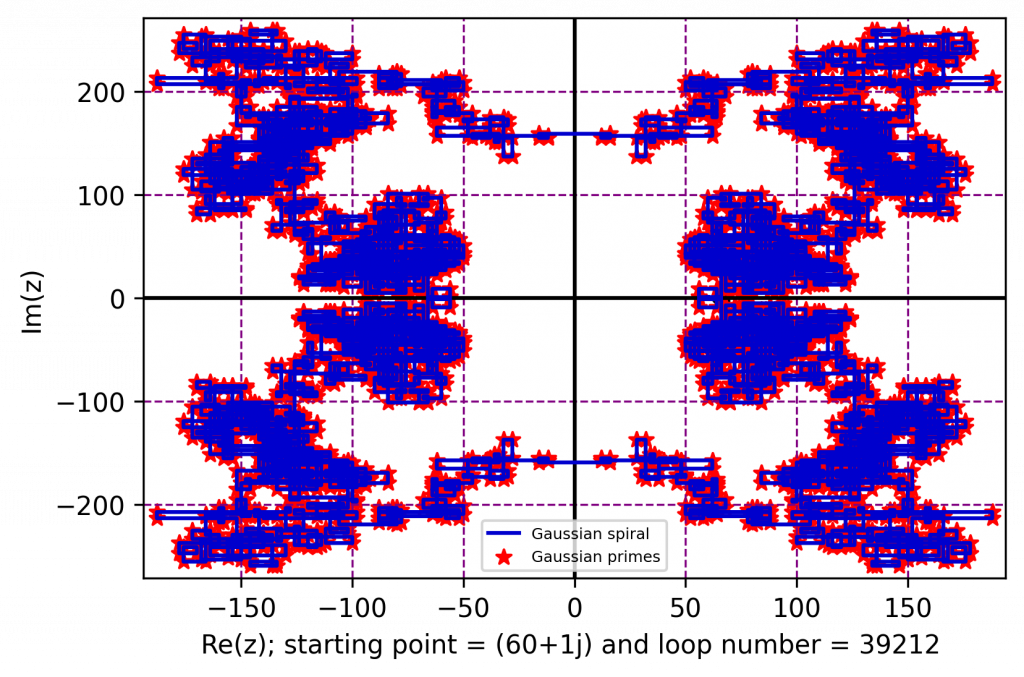
Note: If you are curious, the featured image is actually a visual representation of this collatz conjecture \ $3n+1$ conjecture. You can find the code here.
Statement and Some Examples
The statement of this conjecture can be given like this:
Suppose, we have any random positive integer $n$, we now use two operations:
- If the number n is even, divide it by $2$.
- If the number is odd, triple it and add $1$.
Mathematically, we can write it like this:
$f(n) = \frac{n}{2}$ if $n \equiv 0$ (mod 2)
$ f(n) = (3n+1) $ if $n \equiv 1$ (mod 2)
Now, this conjecture says that no-matter what value of n you choose, you will always get 1 at the end of this operation if you perform it again and again.
Let's take an example, suppose we take $n=12$. As $12$ is an even number, we divide it by $2$. $\frac{12}{2} = 6$, which is again even. So, we again divide it by $2$. This time we get, $\frac{6}{2} = 3$, which is odd, hence, we multiply it by 3 and add $1$, i.e., $3\times 3 + 1 = 10$, which is again even. Hence, repeating this process we get the series $5 \to 16 \to 8 \to 4 \to 2 \to 1$. Seems easy right?,
Let's take again, another number $n=19$. This one gives us $19 \to 58 \to 29 \to 88 \to 44 \to 22 \to 11 \to 34 \to 17 \to 52 \to 26 \to 13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1$. Again at the end we get $1$.
This time, we get much bigger numbers. There is a nice trick to visualize the high values, the plot which we use to do this is called Hailstone Plot.
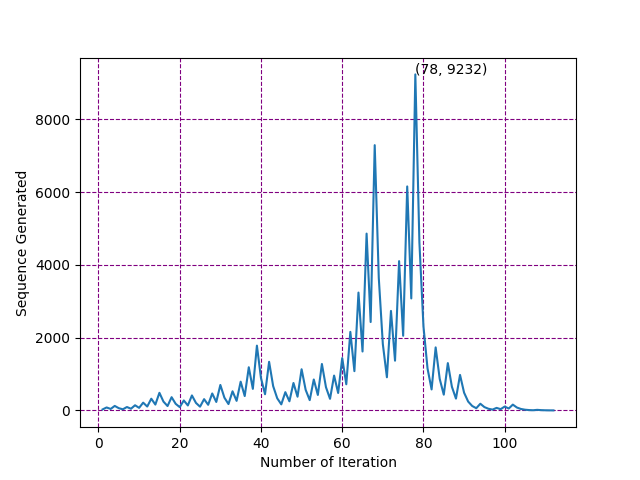
Let's take the number $n=27$. For this number, the list is $27 \to 82 \to 41 \to 124 \to 62 \to 31 \to 94 \to 47 \cdots \to 9232 \cdots$. As you can see, for this number it goes almost as high as 9232 but again it falls down to $1$. The hailstone plot for this is given below.
So, what do you think is the conjecture holds for all number? , no one actually knows. Although, using powerful computers, we have verified this upto $2^{68}$. So, if you are looking for a counterexample, start from 300 quintillion!!
Generating the series for Collatz Conjecture for any number n using python
Let's start with coding part. We will be using numpy library.
import numpy as np
def collatz(n):
result = np.array([n])
while n >1:
# print(n)
if n%2 == 0:
n = n/2
else:
n = 3*n + 1
result = np.append(result,n)
return resultThe function above takes any number $n$ as it's argument. Then, it makes an array (think it as a box of numbers). It creates a box and then put $n$ inside it.
- Then for $n>1$, it check if $n$ is even or not.
- After this, if it is even then $n$ is divided by 2 and the previous value of n is replaced by $\frac{n}{2}$.
- And if $n$ is odd, the it's value is replaced by $3n+1$.
- For each case, we add the value of new $n$ inside our box of number. This whole process run until we have the value of $n=1$.
- Finally, we have the box of all number / series of all number inside the array result.
Let's see the result for $n = 12$.
n = 12
print(collatz(n))
#The output is: [12. 6. 3. 10. 5. 16. 8. 4. 2. 1.]Similarly, for $n = 19$, the code gives us,
n = 19
print(collatz(n))
#The output is: [19. 58. 29. 88. 44. 22. 11. 34. 17. 52. 26. 13. 40. 20. 10. 5. 16. 8. 4. 2. 1.]You can try out the code, it will give you the result for any number $n$.
Test this function.
Hailstone Plot
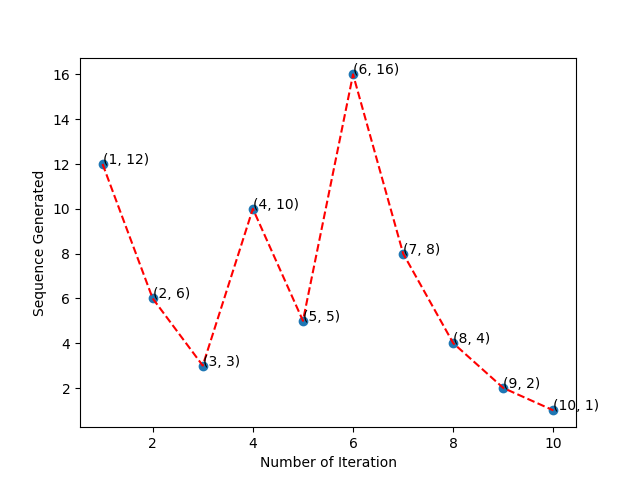
Now let's see how to plot Hailstone plot. Suppose, we have $n = 12$. In the image below, I have shown the series we get from $12$ using the algorithm.

Now, as shown in the above image, we can assign natural numbers on each one of them as shown. So, Now we have two arraies (boxes), one with the series of numbers generated from $n$ and other one from the step number of the applied algorithm, i.e., series of natural numbers. Now, we can take elements from each series one by one and can generate pairs, i.e., two dimensional coordinates.

As shown in the above image, we can generate the coordinates using the steps as x coordinate and series a y coordinate. Now, if we plot the points, then that will give me Hailstone plot. For $n = 12$, we will get something like the image given below. Here I have simply added each dots with a red line.
The code to generate it is quite easy. We will be using matplotlib. We will just simply plot it and will mark the highest value along with it's corresponding step.
import numpy as np
import matplotlib.pyplot as plt
def collatz(n):
result = np.array([n])
while n >1:
# print(n)
if n%2 == 0:
n = n/2
else:
n = 3*n + 1
result = np.append(result,n)
return result
n = 63728127
y_vals = collatz(n); x_vals = np.arange(1,len(y_vals)+1)
plt.plot(x_vals,y_vals)
x_val_max = np.where(y_vals == max(y_vals))[0][0]+1
plt.text(x_val_max, max(y_vals), '({}, {})'.format(x_val_max, int(max(y_vals))))
plt.grid(color='purple',linestyle='--')
plt.ylabel("Sequence Generated")
plt.xlabel("Number of Iteration")
plt.show()The output image is given below.
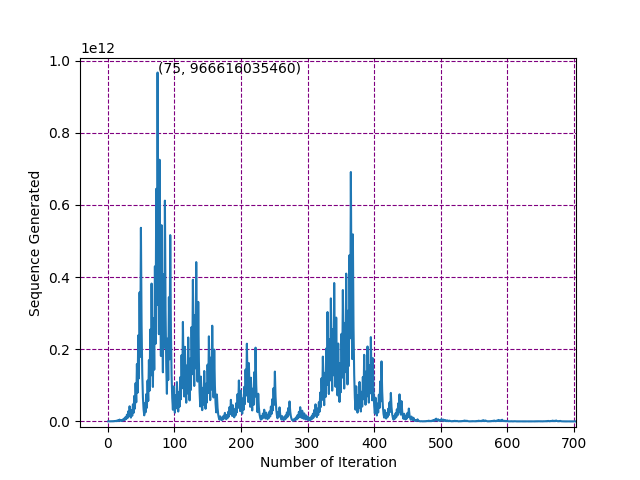
Crazy right?, you can try it out. It's almost feels like some sort of physics thing right!, for some it seems like stock market.
This is all for today. In it's part-2, we will go into much more detail. I hope you have learn something new.
Maybe in the part-2, we will see how to create pattern similar to this using collatz conjecture.