IOQM 2025 Questions, Answer Key, Solutions

Answer Key

Answer 1
40		Answer 2
17		Answer 3
18		Answer 4
5		Answer 5
36
Answer 6
18		Answer 7
576		Answer 8
44		Answer 9
28		Answer 10
15
Answer 11
80		Answer 12
38		Answer 13
13		Answer 14
11		Answer 15
75
Answer 16
8		Answer 17
8		Answer 18
1		Answer 19
72		Answer 20
42
Answer 21
80		Answer 22
7		Answer 23
19		Answer 24
66		Answer 25
9
Answer 26
6		Answer 27
37		Answer 28
12		Answer 29
33		Answer 30
97

Problem 1

If $60 \%$ of a number $x$ is 40 , then what is $x \%$ of 60 ?

Problem 2

Find the number of positive integers $n$ less than or equal to 100 , which are divisible by 3 but are not divisible by 2.

Problem 3

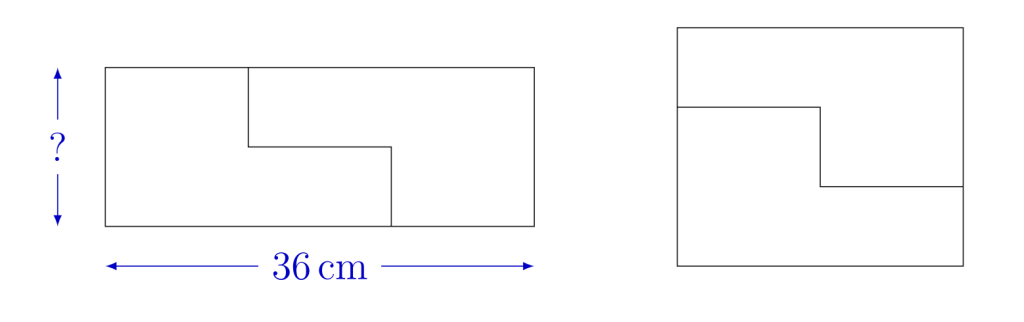
The area of an integer-sided rectangle is 20 . What is the minimum possible value of its perimeter?

Problem 4

How many isosceles integer-sided triangles are there with perimeter 23?

Problem 5

How many 3 -digit numbers $a b c$ in base 10 are there with $a \neq 0$ and $c=a+b$ ?

Problem 6

The height and the base radius of a closed right circular cylinder are positive integers and its total surface area is numerically equal to its volume. If its volume is $k \pi$ where $k$ is a positive integer, what is the smallest possible value of $k$ ?

Problem 7

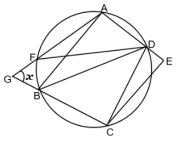
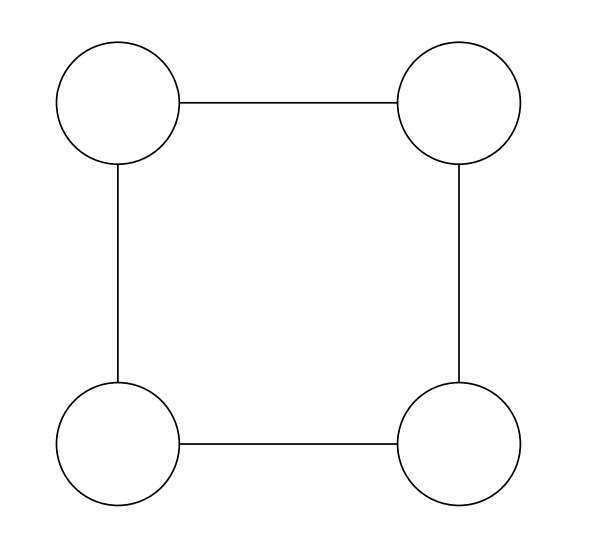
A quadrilateral has four vertices $A, B, C, D$. We want to colour each vertex in one of the four colours red, blue, green or yellow, so that every side of the quadrilateral and the diagonal $A C$ have end points of different colours. In how many ways can we do this?

Problem 8

The sum of two real numbers is a positive integer $n$ and the sum of their squares is $n+1012$. Find the maximum possible value of $n$.

Problem 9

Four sides and a diagonal of a quadrilateral are of lengths $10, 20, 28, 50, 75$, not necessarily in that order. Which amongst them is the only possible length of the diagonal?

Problem 10

The age of a person (in years) in 2025 is a perfect square. His age (in years) was also a perfect square in 2012. His age (in years) will be a perfect cube $m$ years after 2025. Determine the smallest value of $m .=15$

Problem 11

There are six coupons numbered 1 to 6 and six envelopes, also numbered 1 to 6 . The first two coupons are placed together in any one envelope. Similarly, the third and the fourth are placed together in a different envelope, and the last two are placed together in yet another different envelope. How many ways can this be done if no coupon is placed in the envelope having the same number as the coupon?

Problem 12

Consider five-digit positive integers of the form $\overline{a b c a b}$ that are divisible by the two digit number $a b$ but not divisible by 13 . What is the largest possible sum of the digits of such a number?

Problem 13

A function $f$ is defined on the set of integers such that for any two integers $m$ and $n$,

$$
f(m n+1)=f(m) f(n)-f(n)-m+2
$$

holds and $f(0)=1$. Determine the largest positive integer $N$ such that $\sum_{k=1}^N f(k)<100$ .

Problem 14

Consider a fraction $\frac{a}{b} \neq \frac{3}{4}$, where $a, b$ are positive integers with $\operatorname{gcd}(a, b)=1$ and $b \leq 15$. If this fraction is chosen closest to $\frac{3}{4}$ amongst all such fractions, then what is the value of $a+b$ ?

Problem 15

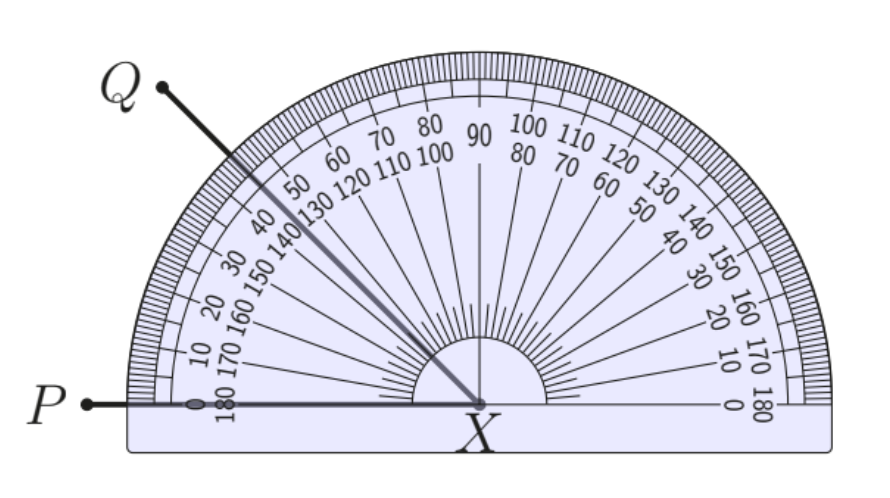
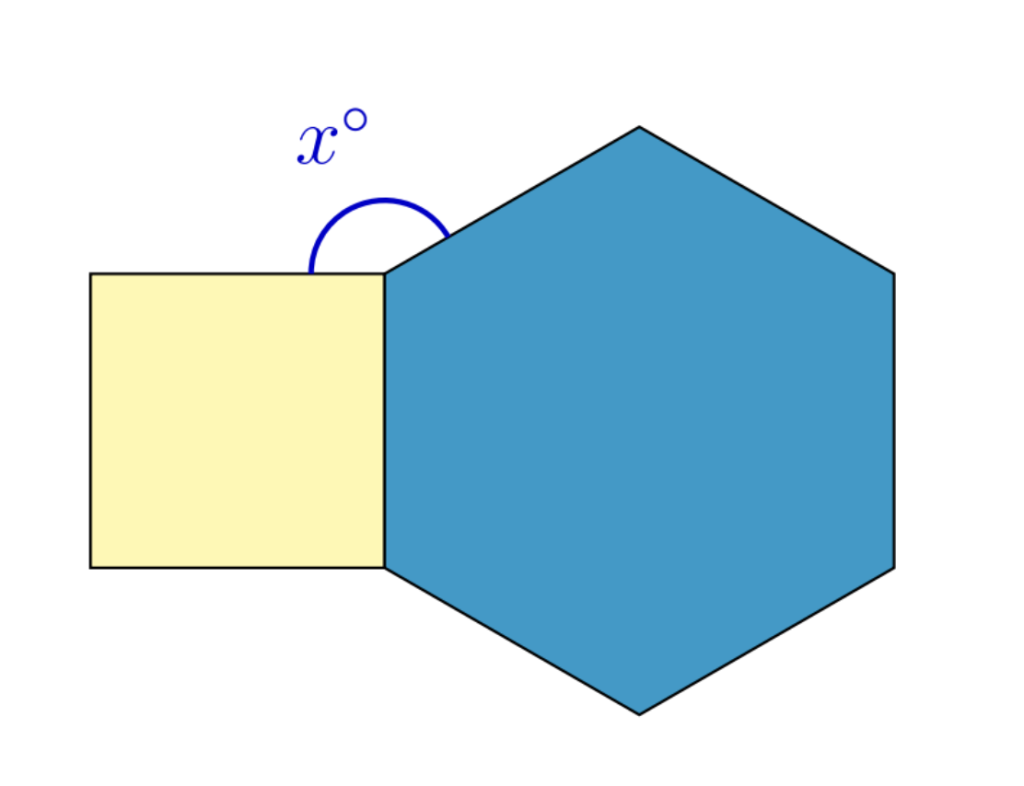
Three sides of a quadrilateral are $a=4 \sqrt{3}, b=9$ and $c=\sqrt{3}$. The sides $a$ and $b$ enclose an angle of $30^{\circ}$, and the sides $b$ and $c$ enclose an angle of $90^{\circ}$. If the acute angle between the diagonals is $x^{\circ}$, what is the value of $x$ ?

Problem 16

$f(x)$ and $g(x)$ be two polynomials of degree 2 such that

$$
\frac{f(-2)}{g(-2)}=\frac{f(3)}{g(3)}=4
$$

If $g(5)=2, f(7)=12, g(7)=-6$, what is the value of $f(5)$ ?

Problem 17

The triangle $A B C, \angle B=90^{\circ}, A B=1$ and $B C=2$. On the side $B C$ there are two points $D$ and $E$ such that $E$ lies between $C$ and $D$ and $D E F G$ is a square, where $F$ lies on $A C$ and $G$ lies on the circle through $B$ with centre $A$. If the area of $D E F G$ is $\frac{m}{n}$ where $m$ and $n$ are positive integers with $\operatorname{gcd}(m, n)=1$, what is the value of $m+n$ ?

Problem 18

$M T A I$ is a parallelogram of area $\frac{40}{41}$ square units such that $M I=1 / M T$. If $d$ is the least possible length of the diagonal $M A$, and $d^2=\frac{a}{b}$, where $a, b$ are positive integers with $\operatorname{gcd}(a, b)=1$, find $|a-b|$.

Problem 19

Let $N$ be the number of nine-digit integers that can be obtained by permuting the digits of 223334444 and which have at least one 3 to the right of the right-most occurrence of 4 . What is the remainder when $N$ is divided by $100$?

Problem 20

Let $f$ be the function defined by

$$
f(n)=\text { remainder when } n^n \text { is divided by } 7,
$$

for all positive integers $n$. Find the smallest positive integer $T$ such that $f(n+T)=f(n)$ for all positive integers $n$.

Problem 21

Let $P(x)=x^{2025}, Q(x)=x^4+x^3+2 x^2+x+1$. Let $R(x)$ be the polynomial remainder when the polynomial $P(x)$ is divided by the polynomial $Q(x)$. Find $R(3)$.

Problem 22

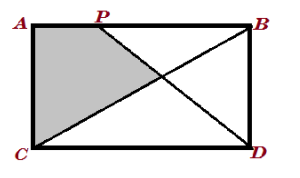
Let $A B C D$ be a rectangle and let $M, N$ be points lying on sides $A B$ and $B C$, respectively. Assume that $M C= C D$ and $M D=M N$, and that points $C, D, M, N$ lic on a circle. If $(A B / B C)^2=m / n$ where $m$ and $n$ are positive integers with $\operatorname{gcd}(m, n)=1$, what is the value of $m+n$ ?

Problem 23

Let \(A B C D\) be a rectangle and let \(M, N\) be points lying on sides \(A B\) and \(B C\), respectively. Assume that \(M C= C D\) and \(M D=M N\), and that points \(C, D, M, N\) lie on a circle. If \((A B / B C)^2=m / n\) where \(m\) and \(n\) are positive integers with \(\operatorname{gcd}(m, n)=1\), what is the value of \(m+n\) ?

Problem 24

There are $m$ blue marbles and $n$ red marbles on a table. Armaan and Babita play a game by taking turns. In each turn the player has to pick a marble of the colour of his/her choice. Armaan starts first, and the player who picks the last red marble wins. For how many choices of $(m, n)$ with $1 \leq m, n \leq 11$ can Armaan force a win?

Problem 25

For some real numbers $m, n$ and a positive integer $a$, the list $(a+1) n^2, m^2, a(n+1)^2$ consists of three consecutive integers written in increasing order. What is the largest possible value of $m^2$ ?

Problem 26

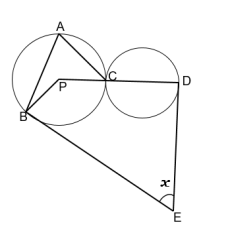
Let $S$ be a circle of radius 10 with centre $O$. Suppose $S_1$ and $S_2$ are two circles which touch $S$ internally and intersect each other at two distinct points $A$ and $B$. If $\angle O A B=90^{\circ}$ what is the sum of the radii of $S_1$ and $S_2$ ?

Solution

Problem 27

A regular polygon with $n \geq 5$ vertices is said to be colourful if it is possible to colour the vertices using at most 6 colours such that each vertex is coloured with exactly one colour, and such that any 5 consecutive vertices have different colours. Find the largest number $n$ for which a regular polygon with $n$ vertices is not colourful.

Solution

Problem 28

Find the number of ordered triples $(a, b, c)$ of positive integers such that $1 \leq a, b, c \leq 50$ which satisfy the relation

$$
\frac{\operatorname{lcm}(a, c)+\operatorname{lcm}(b, c)}{a+b}=\frac{26 c}{27}
$$

Here, by $\operatorname{lcm}(x, y)$ we mean the LCM, that is, least common multiple of $x$ and $y$.

Problem 29

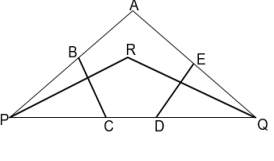
Consider a sequence of real numbers of finite length. Consecutive four term averages of this sequence are strictly increasing, but consecutive seven term averages are strictly decreasing. What is the maximum possible length of such a sequence?

Problem 30

Assume $a$ is a positive integer which is not a perfect square. Let $x, y$ be non-negative integers such that $\sqrt{x-\sqrt{x+a}}=\sqrt{a}-y$. What is the largest possible value of $a$ such that $a<100 ?$

BHASKARA Contest - NMTC - Screening Test – 2025

Problem 1

The greatest 4 -digit number such that when divided by 16,24 and 36 leaves 4 as remainder in each case is
А) 9994
B) 9940
C) 9094
D) 9904

Problem 2

\(A B C D\) is a rectangle whose length \(A B\) is 20 units and breadth is 10 units. Also, given \(A P=8\) units. The area of the shaded region is \(\frac{p}{q}\) sq unit, where \(p, q\) are natural numbers with no common factors other than 1 . The value of \(p+q\) is
A) 167
В) 147
C) 157
D) 137

Problem 3

The solution of \(\frac{\sqrt[7]{12+x}}{x}+\frac{\sqrt[7]{12+x}}{12}=\frac{64}{3}(\sqrt[7]{x})\) is of the form \(\frac{a}{b}\) where \(a, b\) are natural numbers with \(\operatorname{GCD}(a, b)=1\); then \((b-a)\) is equal to
A) 115
B) 114
C) 113
D) 125

Problem 4

The value of \((52+6 \sqrt{43})^{3 / 2}-(52-6 \sqrt{43})^{3 / 2}\) is
A) 858
В) 918
C) 758
D) 828

Problem 5

In the adjoining figure \(\angle D C E=10^{\circ}\), \(\angle C E D=98^{\circ}, \angle B D F=28^{\circ}\)
Then the measure of angle \(x\) is
A) \(72^{\circ}\)
B) \(76^{\circ}\)
C) \(44^{\circ}\)
D) \(82^{\circ}\)

Problem 6

\(A B C\) is a right triangle in which \(\angle \mathrm{B}=90^{\circ}\). The inradius of the triangle is \(r\) and the circumradius of the triangle is R . If \(\mathrm{R}: r=5: 2\), then the value of \(\cot ^2 \frac{A}{2}+\cot ^2 \frac{C}{2}\) is
A) \(\frac{25}{4}\)
B) 17
C) 13
D) 14

Problem 7

If \((\alpha, \beta)\) and \((\gamma, \beta)\) are the roots of the simultaneous equations:

\[
|x-1|+|y-5|=1 ; \quad y=5+|x-1|
\]

then the value of \(\alpha+\beta+\gamma\) is
A) \(\frac{15}{2}\)
B) \(\frac{17}{2}\)
C) \(\frac{14}{3}\)
D) \(\frac{19}{2}\)

Problem 8

Three persons Ram, Ali and Peter were to be hired to paint a house. Ram and Ali can paint the whole house in 30 days, Ali and Peter in 40 days while Peter and Ram can do it in 60 days. If all of them were hired together, in how many days can they all three complete $50 \%$ of the work?
A) $24 \frac{1}{3}$
B) $25 \frac{1}{2}$
C) $26 \frac{1}{3}$
D) $26 \frac{2}{3}$

Problem 9

$\frac{\sqrt{a+3 b}+\sqrt{a-3 b}}{\sqrt{a+3 b}-\sqrt{a-3 b}}=x$, then the value of $\frac{3 b x^2+3 b}{a x}$ is
A) 1
B) 2
C) 3
D) 4

Problem 10

The number of integral solutions of the inequation $\left|\frac{2}{x-13}\right|>\frac{8}{9}$ is
A) 1
B) 2
C) 3
D) 4

Problem 11

In the adjoining figure, $P$ is the centre of the first circle, which touches the other circle in C . PCD is along the diameter of the second circle. $\angle \mathrm{PBA}=20^{\circ}$ and $\angle \mathrm{PCA}=30^{\circ}$.

The tangents at B and D meet at E . The measure of the angle $x$ is
A) $75^{\circ}$
B) $80^{\circ}$
C) $70^{\circ}$
D) $85^{\circ}$

Problem 12

If $\alpha, \beta$ are the values of $x$ satisfying the equation $3 \sqrt{\log _2 x}-\log _2 8 x+1=0$, where $\alpha<\beta$, then the value of $\left(\frac{\beta}{\alpha}\right)$ is
A) 2
B) 4
C) 6
D) 8

Problem 13

When a natural number is divided by 11 , the remainder is 4 . When the square of this number is divided by 11 , the remainder is
A) 4
B) 5
C) 7
D) 9

Problem 14

The unit's digit of a 2-digit number is twice the ten's digit. When the number is multiplied by the sum of the digits the result is 144 . For another 2-digit number, the ten's digit is twice the unit's digit and the product of the number with the sum of its digits is 567 . Then the sum of the two 2 -digit numbers is
A) 68
В) 86
C) 98
D) 87

Problem 15

$A B C D E$ is a pentagon. $\angle A E D=126^{\circ}, \angle B A E=\angle C D E$ and $\angle A B C$ is $4^{\circ}$ less than $\angle B A E$ and $\angle B C D$ is $6^{\circ}$ less than $\angle C D E . P R, Q R$ the bisectors of $\angle B P C, \angle E Q D$ respectively, meet at $R$. Points $\mathrm{P}, \mathrm{C}, \mathrm{D}, \mathrm{Q}$ are collinear. Then measure of $\angle P R Q$ is
A) $151^{\circ}$
B) $137^{\circ}$
C) $141^{\circ}$
D) $143^{\circ}$

Problem 16

$a, b, c$ are real numbers such that $b-c=8$ and $b c+a^2+16=0$.
The numerical value of $a^{2025}+b^{2025}+c^{2025}$ is $\rule{2cm}{0.2mm}$.

Problem 17

Given $f(x)=\frac{2025 x}{x+1}$ where $x \neq-1$. Then the value of $x$ for which $f(f(x))=(2025)^2$ is $\rule{2cm}{0.2mm}$.

Problem 18

The sum of all the roots of the equation $\sqrt[3]{16-x^3}=4-x$ is $\rule{2cm}{0.2mm}$.

Problem 19

In the adjoining figure, two
Quadrants are touching at $B$.
$C E$ is joined by a straight line, whose mid-point is $F$.

The measure of $\angle C E D$ is $\rule{2cm}{0.2mm}$.

Problem 20

The value of $k$ for which the equation $x^3-6 x^2+11 x+(6-k)=0$ has exactly three positive integer solutions is $\rule{2cm}{0.2mm}$.

Problem 21

The number of 3-digit numbers of the form $a b 5$ (where $a, b$ are digits) which are divisible by 9 is $\rule{2cm}{0.2mm}$.

Problem 22

If $a=\sqrt{(2025)^3-(2023)^3}$, the value of $\sqrt{\frac{a^2-2}{6}}$ is $\rule{2cm}{0.2mm}$.

Problem 23

In a math Olympiad examination, $12 \%$ of the students who appeared from a class did not solve any problem; $32 \%$ solved with some mistakes. The remaining 14 students solved the paper fully and correctly. The number of students in the class is $\rule{2cm}{0.2mm}$.

Problem 24

When $a=2025$, the numerical value of
$\left|2 a^3-3 a^2-2 a+1\right|-\left|2 a^3-3 a^2-3 a-2025\right|$ is $\rule{2cm}{0.2mm}$.

Problem 25

A circular hoop and a rectangular frame are standing on the level ground as shown. The diagonal $A B$ is extended to meet the circular hoop at the highest point $C$. If $A B=18 \mathrm{~cm}, B C=32 \mathrm{~cm}$, the radius of the hoop (in cm ) is $\rule{2cm}{0.2mm}$.

Problem 26

' $n$ ' is a natural number. The number of ' $n$ ' for which $\frac{16\left(n^2-n-1\right)^2}{2 n-1}$ is a natural number is $\rule{2cm}{0.2mm}$.

Problem 27

The number of solutions $(x, y)$ of the simultaneous equations $\log _4 x-\log _2 y=0, \quad x^2=8+2 y^2$ is $\rule{2cm}{0.2mm}$.

Problem 28

In the adjoining figure,
$P A, P B$ are tangents.
$A R$ is parallel to $P B$

$P Q=6 ; Q R=18 .$

Length $S B= \rule{2cm}{0.2mm}$.

Problem 29

A large watermelon weighs 20 kg with $98 \%$ of its weight being water. It is left outside in the sunshine for some time. Some water evaporated and the water content in the watermelon is now $95 \%$ of its weight in water. The reduced weight in kg is $\rule{2cm}{0.2mm}$.

Problem 30

In a geometric progression, the fourth term exceeds the third term by 24 and the sum of the second and third term is 6 . Then, the sum of the second, third and fourth terms is $\rule{2cm}{0.2mm}$.

Australian Mathematics Competition - 2019 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

$201-9=$

(A) 111 (B) 182 (C) 188 (D) 192 (E) 198

Problem 2:

A Runnyball team has 5 players. This graph shows the number of goals each player scored in a tournament. Who scored the second-highest number of goals?


(A) Ali (B) Beth (C) Caz (D) Dan (E) Evan

Problem 3:

Six million two hundred and three thousand and six would be written as

(A) 62036 (B) 6230006 (C) 6203006 (D) 6203600 (E) 6200306

Problem 4:

These cards were dropped on the table, one at a time. In which order were they dropped?

Problem 5:

Sophia is at the corner of 1st Street and 1st Avenue. Her school is at the corner of 4th Street and 3rd Avenue. To get there, she walks



(A) 4 blocks east, 3 blocks north (B) 3 blocks west, 4 blocks north (C) 4 blocks west, 2 blocks north (D) 3 blocks east, 2 blocks north (E) 2 blocks north, 2 blocks south

Problem 6:

Jake is playing a card game, and these are his cards. Elena chooses one card from Jake at random. Which of the following is Elena most likely to choose?

Problem 7:

Which 3D shape below has 5 faces and 9 edges?

Problem 8:

We're driving from Elizabeth to Renmark, and as we leave we see this sign. We want to stop at a town for lunch and a break, approximately halfway to Renmark. Which town is the best place to stop?

(A) Gawler (B) Nuriootpa (C) Truro (D) Blanchetown (E) Waikerie

Problem 9:

What is the difference between the heights of the two flagpoles, in metres?


(A) 16.25 (B) 16.75 (C) 17.25 (D) 17.75 (E) 33.25

Problem 10:

Most of the numbers on this scale are missing.

Which number should be at position $P$ ?
(A) 18 (B) 33 (C) 34 (D) 36 (E) 42

Problem 11:

In a game, two ten-sided dice each marked 0 to 9 are rolled and the two uppermost numbers are added. For example, with the dice as shown, $0+9=9$. How many different results can be obtained?

(A) 17 (B) 18 (C) 19 (D) 20 (E) 21

Problem 12:

Every row and every column of this $3 \times 3$ square must contain each of the numbers 1,2 and 3 . What is the value of $N+M$ ?

(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

Problem 13:

Ada Lovelace and Charles Babbage were pioneering researchers into early mechanical computers. They were born 24 years apart.

To the nearest year, how much longer did Charles Babbage live than Ada Lovelace?

(A) 29 (B) 32 (C) 35 (D) 37 (E) 43

Problem 14:

You have 12 metres of ribbon. Each decoration needs $\frac{2}{5}$ of a metre of ribbon. How many decorations can you make?

(A) 6 (B) 7 (C) 10 (D) 24 (E) 30

Problem 15:

Andrew and Bernadette are clearing leaves from their backyard. Bernadette can rake the backyard in 60 minutes, while Andrew can do it in 30 minutes with the vacuum setting on the leaf blower. If they work together, how many minutes will it take?

(A) 10 (B) 20 (C) 24 (D) 30 (E) 45

Problem 16:

A carpet tile measures 50 cm by 50 cm . How many of these tiles would be needed to cover the floor of a room 6 m long and 4 m wide?

(A) 24 (B) 20 (C) 40 (D) 48 (E) 96

Problem 17:

In how many different ways can you place the numbers 1 to 4 in these four circles so that no two consecutive numbers are side by side?

(A) 2 (B) 4 (C) 6 (D) 8 (E) 12

Problem 18:

John, Chris, Anne, Holly and Mike are seated around a round table, each with a card with a number on it in front of them. Each person can see the numbers in front of their two neighbours. Each person calls out the sum of the two numbers in front of their neighbours. John says 30, Chris says 33, Anne says 31, Holly says 38 and Mike says 36. Holly has the number 21 in front of her. What number does Anne have in front of her?

(A) 9 (B) 13 (C) 15 (D) 18 (E) 19

Problem 19:

Annabel has 2 identical equilateral triangles. Each has an area of $9 \mathrm{~cm}^2$. She places one triangle on top of the other as shown to form a star, as shown. What is the area of the star in square centimetres?


(A) 10 (B) 12 (C) 14 (D) 16 (E) 18

Problem 20:

Lola went on a train trip. During her journey she slept for $\frac{3}{4}$ of an hour and stayed awake for $\frac{3}{4}$ of the journey. How long did the trip take?

(A) 1 hour (B) 2 hours (C) $2 \frac{1}{2}$ hours (D) 3 hours (E) 4 hours

Problem 21:

My sister and I are playing a game where she picks two counting numbers and I have to guess them. When I tell her a number, she multiplies my number by her first number and then adds her second number. When I say 15 , she says 50 . When I say 2 , she says 11 . If I say 6 , what should she say?

(A) 23 (B) 27 (C) 35 (D) 41 (E) 61

Problem 22:

Once the muddy water from the 2018 Ingham floods had drained from Harry's house, he found this folded map that had been standing in the floodwater at an angle. He unfolded it and laid it out to dry, but it was still mud-stained. What could it look like now?

Problem 23:

A tower is built from exactly 2019 equal rods. Starting with 3 rods as a triangular base, more rods are added to form a regular octahedron with this base as one of its faces. The top face is then the base of the next octahedron. The diagram shows the construction of the first three octahedra. How many octahedra are in the tower when it is finished?

(A) 2016 (B) 1008 (C) 336 (D) 224 (E) 168

Problem 24:

These three cubes are labelled in exactly the same way, with the 6 letters A, M, C, D, E and F on their 6 faces:


The cubes are now placed in a row so that the front looks like this:

When we look at the cubes from the opposite side, we will see

Problem 25:

In Jeremy's hometown of Windar, people live in either North, East, South, West or Central Windar. Jeremy is putting together a chart showing where the students in his class live, but unfortunately his dog chewed his survey results before he managed to label the five columns.


He only remembers two things about the survey: South Windar is more common than both East and Central Windar, and the number of students in North and Central Windar combined is the same as the total of the other three regions.
Using only this information, how many columns can Jeremy correctly label with \(100 \%\) certainty?

(A) 0 (B) 1 (C) 2 (D) 3 (E) 5

Problem 26:

Pip starts with a large square sheet of paper and makes two straight cuts to form four smaller squares. She then takes one of these smaller squares and makes two more straight cuts to make four even smaller ones, as shown.

Continuing in this way, how many cuts does Pip need to make to get a total of 1000 squares of various sizes?

Problem 27:

Seven of the numbers from 1 to 9 are placed in the circles in the diagram in such a way that the products of the numbers in each vertical or horizontal line are the same. What is this product?

Problem 28:

A hare and a tortoise compete in a 10 km race. The hare runs at \(30 \mathrm{~km} / \mathrm{h}\) and the tortoise walks at \(3 \mathrm{~km} / \mathrm{h}\). Unfortunately, at the start, the hare started running in the opposite direction. After some time, it realised its mistake and turned round, catching the tortoise at the halfway mark. For how many minutes did the hare run in the wrong direction?

Problem 29:

I want to place the numbers 1 to 10 in this diagram, with one number in each circle. On each of the three sides, the four numbers add to a side total, and the three side totals are all the same. What is the smallest number that this side total could be?

Problem 30:

The sum of two numbers is 11.63 . When adding the numbers together, Oliver accidentally shifted the decimal point in one of the numbers one position to the left. Oliver got an answer of 5.87 instead. What is one hundred times the difference between the two original numbers?

Australian Mathematics Competition - 2020 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

How many pieces have been placed in the jigsaw puzzle so far?

(A) 25 (B) 27 (C) 30 (D) 33 (E) 35

Problem 2:

What is half of 2020 ?

(A) 20 (B) 101 (C) 110 (D) 1001 (E) 1010

Problem 3:

What is the perimeter of this triangle?

(A) 33 m (B) 34 m (C) 35 m (D) 36 m (E) 37 m

Problem 4:

Which fraction is the largest?

(A) one-half (B) one-quarter (C) one-third (D) three-quarters (E) six-tenths

Problem 5:

A protractor is used to measure angle (P X Q). The angle is

(A) $45^{\circ}$ (B) $55^{\circ}$ (C) $135^{\circ}$ (D) $145^{\circ}$ (E) $180^{\circ}$

Problem 6:

Some friends are walking to a lake in the mountains. First they climb a hill before they walk down to the lake. Which graph most accurately represents their journey?

Problem 7:

How many tenths are in 6.2 ?

(A) 62 (B) 8 (C) 4 (D) 12 (E) 36

Problem 8:

The graph shows the number of eggs laid by backyard chickens Nony and Cera for the first six months of the year.

In how many months did Nony lay more eggs than Cera?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 9:

A class of 24 students, all of different heights, is standing in a line from tallest to shortest. Mary is the 8th tallest and John is the 6 th shortest. How many students are standing between them in the line?

(A) 6 (B) 7 (C) 8 (D) 9 (E) 10

Problem 10:

Maria divided a rectangle into a number of identical squares and coloured some of them in, as shown. She wants three-quarters of the rectangle's area to be coloured in altogether. How many more squares does she need to colour in?


(A) 0 (B) 1 (C) 2 (D) 3 (E) 4

Problem 11:

At the end of a game of marbles, Lei has 15 marbles, Dora has 8 and Omar has 4 . How many marbles must Lei give back to his friends if they want to start the next game with an equal number each?

(A) 5 (B) 6 (C) 7 (D) 8 (E) 9

Problem 12:

In the grid, the total of each row is given at the end of the row, and the total of each column is given at the bottom of the column.
The value of $N$ is

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 13:

At his birthday party, Ricky and his friends wear stripy paper hats in the shape of a cone, as shown on the left. After the party, Ricky makes a straight cut in one of the hats all the way up to the point at the top, as shown on the right.

Which of the following best matches what the hat will look like when Ricky flattens it out on the table?

Problem 14:

Emma is going to write all the numbers from 1 to 50 in order. She writes 25 digits on the first line of her page. What was the last number she wrote on this line?

(A) 13 (B) 15 (C) 17 (D) 19 (E) 21

Problem 15:

The playing card shown is flipped over along edge $b$ and then flipped over again along edge $c$. What does it look like now?

Problem 16:

Which labelled counter should you remove so that no two rows have the same number of counters and no two columns have the same number of counters?

Problem 17:

Aidan puts a range of 3D shapes on his desk at school. This is the view from his side of the desk:

Nadia is sitting on the opposite side of the desk facing Aidan. Which of the following diagrams best represents the view from Nadia's side of the desk?

Problem 18:

The area of each of the five equilateral triangles in the diagram is 1 square metre. What is the shaded area?

(A) $1.5 \mathrm{~m}^2$ (B) $2 \mathrm{~m}^2$ (C) $2.5 \mathrm{~m}^2$ (D) $3 \mathrm{~m}^2$ (E) $3.5 \mathrm{~m}^2$

Problem 19:

Kayla is 5 years old and Ryan is 13 years younger than Cody. One year ago, Cody's age was twice the sum of Kayla's and Ryan's age. Find the sum of the three children's current ages.

(A) 10 (B) 22 (C) 26 (D) 30 (E) 36

Problem 20:

Mary has a piece of paper. She folds it exactly in half. Then she folds it in half again. She finishes up with this shape.

Which of the shapes $P, Q$ and $R$ shown below could have been her starting shape?

(A) only $P$ (B) only $Q$ (C) only $R$ (D) only $P$ and $R$ (E) all three

Problem 21:

Four positive whole numbers are placed at the vertices of a square. On each edge, the difference between the two numbers at the vertices is written. The four edge numbers are $1,2,3$ and 4 in some order. What is the smallest possible sum of the numbers at the vertices?

(A) 10 (B) 11 (C) 12 (D) 13 (E) 14

Problem 22:

The large rectangle shown has been divided into 4 smaller rectangles. The perimeters of three of these are $10 \mathrm{~cm}, 16 \mathrm{~cm}$ and 20 cm . The fourth rectangle does not have the largest or the smallest perimeter of the four smaller rectangles.

What, in centimetres, is the perimeter of the large rectangle?

(A) 26 (B) 30 (C) 32 (D) 36 (E) 46

Problem 23:

A bale of hay can be eaten by a horse in 2 days, by a cow in 3 days and by a sheep in 12 days. A farmer has 22 bales of hay and one horse, one cow and one sheep to feed. How many days will his bales last?

(A) 20 (B) 22 (C) 24 (D) 26 (E) 28

Problem 24:

This rectangle is 36 cm long. It is cut into two pieces and rearranged to form a square, as shown.


What is the height of the original rectangle?

(A) 14 cm (B) 16 cm (C) 18 cm (D) 20 cm (E) 24 cm

Problem 25:

A bottle with a sealed lid contains some water. The diagram shows this bottle up the right way and upside down. How full is the bottle?


(A) $\frac{1}{2}$ (B) $\frac{4}{7}$ (C) $\frac{5}{7}$ (D) $\frac{2}{3}$ (E) $\frac{9}{14}$

Problem 26:

A number is oddtastic if all of its digits are odd. For example, 9,57 and 313 are oddtastic. However, 50 and 787 are not oddtastic, since 0 and 8 are even digits. How many of the numbers from 1 to 999 are oddtastic?

Problem 27:

On my chicken farm where I have 24 pens, the pens were a bit crowded. So I built 6 more pens, and the number of chickens in each pen reduced by 6 . How many chickens do I have?

Problem 28:

How many even three-digit numbers are there where the digits add up to $8 ?$

Problem 29:

Madeleine types her three-digit Personal Identification Number (PIN) into this keypad. All three digits are different, but the buttons for the first and second digits share an edge, and the buttons for the second and third digits share an edge. For instance, 563 is a possible PIN, but 536 is not, since 5 and 3 do not share an edge. How many possibilities are there for Madeleine's PIN?

Problem 30:

Writing one digit every second, you have half an hour to list as many of the counting numbers as you can, starting $1,2,3, \ldots$. At the end of half an hour, what number have you just finished writing?

Australian Mathematics Competition - 2021 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

This Nigerian flag is white and green. What fraction of it is green?

(A) one-third (B) one-quarter (C) one-half (D) two-fifths (E) two-thirds

Problem 2:

Which number makes this number sentence true? $\square$ -5=9

(A) 0 (B) 4 (C) 12 (D) 9 (E) 14

Problem 3:

What is the perimeter of the quadrilateral shown?

(A) 13 cm (B) 15 cm (C) 17 cm (D) 19 cm (E) 21 cm

Problem 4:

Which of the following decimal numbers has the smallest value?

(A) 0.0002 (B) 0.002 (C) 0.02 (D) 0.2 (E) 2.0

Problem 5:

$\frac{1}{2}+\frac{2}{4}-\frac{4}{8}=$

(A) $\frac{1}{2}$ (B) 1 (C) $1 \frac{1}{2}$ (D) 2 (E) 4

Problem 6:

Suri has a number of 20-cent and 50-cent coins. Which of the following amounts of money is it NOT possible for her to make?

(A) 50 cents (B) 60 cents (C) 80 cents (D) 30 cents (E) 70 cents

Problem 7:

A square of paper is rolled up, pressed flat, and then cut as shown.

What could the sheet of paper look like when unrolled and leid flat?



Problem 8:

Leo is waiting in line at school. There are four students ahead of him and twice as many behind him. How many students are in this line?

(A) 4 (B) 8 (C) 9 (D) 12 (E) 13

Problem 9:

Cassandra makes a healing potion from a mixture of herbs. She uses this balance to weigh out the herbs. If she uses 5 grams of fennel, how many grams of mint will she need?


(A) 5 (B) 10 (C) 15 (D) 20 (E) 40

Problem 10:

There are 14 pieces of fruit in a bowl. There are twice as many nectarines as pears, and half as many nectarines as apples. There are no other types of fruit. How many apples are there?


(A) 2 (B) 4 (C) 6 (D) 8 (E) 10

Problem 11:

I am shuffling a deck of cards but I accidentally drop a card on the ground every now and then. After a while, I notice that I have dropped five cards. From above, the five cards look like one of the following pictures. Which picture could it be?

Problem 12:

This rectangle has been made by joining two squares together. Each square has an area of $25 \mathrm{~cm}^2$. What is the perimeter of the rectangle?

(A) 18 cm (B) 20 cm (C) 26 cm (D) 30 cm (E) 50 cm

Problem 13:

A kangaroo is chasing a wallaby that is 42 metres ahead. For every 4 -metre hop the kangaroo makes, the wallaby makes a 1-metre hop. How many hops will the kangaroo have to make to catch up with the wallaby?

(A) 8 (B) 10 (C) 11 (D) 14 (E) 21

Problem 14:

A piece of straight wire is 50 cm long. Six right-angled bends are made in the wire, so that it ends up looking like the diagram shown:

The lengths of two sections are shown. What is the length marked $x$ ?

(A) 28 cm (B) 31 cm (C) 34 cm (D) 36 cm (E) 39 cm

Problem 15:

Margie and Rosie both live near Lawson train station. Each plans to catch the 10 am train. Margie thinks her watch is 10 minutes fast, but in fact it is 10 minutes slow. Rosie thinks her watch is 10 minutes slow, but in fact it is 5 minutes fast. Each of them leaves home to catch the train without having to wait on the platform. Who misses the train, and by how much?

(A) Margie by 10 minutes (B) Margie by 20 minutes (C) Rosie by 5 minutes (D) Rosie by 15 minutes (E) Neither of them

Problem 16:

Sally was playing with block patterns and came up with this one she called Hollow Squares. They all follow the same pattern.

How many blocks would she need to make Hollow Square 7 ?

(A) 28 (B) 30 (C) 32 (D) 34 (E) 53

Problem 17:

I have a jug containing 100 mL of liquid, which is half vinegar and half olive oil. How much vinegar must I add to make a mixture which is one-third olive oil?

(A) 30 mL (B) 40 mL (C) 50 mL (D) 60 mL (E) 100 mL

Problem 18:

It is 10 am now. What time will it be in 2021 hours time?

(A) 11 am (B) 1 pm (C) 3 pm (D) 4 pm (E) 5 pm

Problem 19:

Alexander's pen leaked on his addition homework, covering up three of the digits in the calculation shown. How many different possibilities are there for the correct working?


(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

Problem 20:

Our school is organising a quiz night. They are expecting from 25 to 35 people to come. The people will be arranged in teams of 6 to 8 people. What is the range of possible numbers of teams to expect?

(A) 4 to 5 (B) 4 to 6 (C) 5 to 6 (D) 3 to 6 (E) 3 to 5

Problem 21:

In an election for school captain, there were 4 candidates and 453 students each voted for one candidate. The winner's margins over the other candidates were 31,25 and 19. How many votes did the winner receive?

(A) 113 (B) 127 (C) 129 (D) 131 (E) 132

Problem 22:

Three blocks with rectangular faces are placed together to form a larger rectangular prism. All blocks have side lengths which are whole numbers of centimetres. The areas of some of the faces are shown, as is the length of one edge.

In cubic centimetres, what is the volume of the combined prism?

(A) 360 (B) 540 (C) 600 (D) 720 (E) 900

Problem 23:

Three gears are connected as shown. The two larger gears have 20 teeth each and the smaller gear has 10 teeth.
The middle gear is rotated half a turn in the direction of the arrows, turning the M upside down.

What do the three gears look like after this rotation?

Problem 24:

Anna has a large number of tiles of three types:


She wants to build a green rectangle with a white frame similar to those below.

She builds such a rectangle using as many tiles as possible while using exactly 20 completely green tiles. How many tiles will she use altogether?

(A) 80 (B) 66 (C) 48 (D) 42 (E) 39

Problem 25:

In Jeremy's hometown of Windar, people live in either North, East, South, West or Central Windar. Jeremy is putting together a chart showing where the students in his class live, but unfortunately his dog chewed his survey results before he managed to label the five columns.


He only remembers two things about the survey: South Windar is more common than both East and Central Windar, and the number of students in North and Central Windar combined is the same as the total of the other three regions. Using only this information, how many columns can Jeremy correctly label with \(100 \%\) certainty?

(A) 0 (B) 1 (C) 2 (D) 3 (E) 5

Problem 26:

Pip starts with a large square sheet of paper and makes two straight cuts to form four smaller squares. She then takes one of these smaller squares and makes two more straight cuts to make four even smaller ones, as shown.

Continuing in this way, how many cuts does Pip need to make to get a total of 1000 squares of various sizes?

Problem 27:

Seven of the numbers from 1 to 9 are placed in the circles in the diagram in such a way that the products of the numbers in each vertical or horizontal line are the same. What is this product?

Problem 28:

A hare and a tortoise compete in a 10 km race. The hare runs at \(30 \mathrm{~km} / \mathrm{h}\) and the tortoise walks at \(3 \mathrm{~km} / \mathrm{h}\). Unfortunately, at the start, the hare started running in the opposite direction. After some time, it realised its mistake and turned round, catching the tortoise at the halfway mark. For how many minutes did the hare run in the wrong direction?

Problem 29:

I want to place the numbers 1 to 10 in this diagram, with one number in each circle. On each of the three sides, the four numbers add to a side total, and the three side totals are all the same. What is the smallest number that this side total could be?

Problem 30:

The sum of two numbers is 11.63 . When adding the numbers together, Oliver accidentally shifted the decimal point in one of the numbers one position to the left. Oliver got an answer of 5.87 instead. What is one hundred times the difference between the two original numbers?

Australian Mathematics Competition - 2022 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

What number is two hundred and five thousand, one hundred and fifty?

(A) 150 (B) 205 (C) 20150 (D) 25150 (E) 205150

Problem 2:

What fraction of this picture is shaded?


(A) $\frac{1}{2}$ (B) $\frac{2}{3}$ (C) $\frac{3}{4}$ (D) $\frac{4}{9}$ (E) $\frac{5}{9}$

Problem 3:

$2220-2022=$

(A) 18 (B) 188 (C) 198 (D) 200 (E) 202

Problem 4:

Audrey wrote these three numbers in order from smallest to largest:

$$
\begin{array}{llll}
1.03 & 0.08 & 0.4
\end{array}
$$

In which order did she write them?

(A) $0.08,1.03,0.4$ (B) $0.08,0.4,1.03$ (C) $0.4,0.08,1.03$
(D) $0.4,1.03, .008$ (E) $1.03,0.4,0.08$

Problem 5:

I was 7 years old when my brother turned 3. How old will I be when
he turns 7?

(A) 9 (B) 10 (C) 11 (D) 12 (E) 13

Problem 6:

This shape is built from 29 squares, each $1 \mathrm{~cm} \times 1 \mathrm{~cm}$. What is its perimeter in centimetres?

(A) 52 (B) 58 (C) 60 (D) 68 (E) 72

Problem 7:

A tachometer indicates how fast the crankshaft in a car's engine is spinning, in thousands of revolutions per minute (rpm). What is the reading on the tachometer shown?



(A) 2.2 rpm (B) 2.4 rpm (C) 240 rpm (D) 2200 rpm (E) 2400 rpm

Problem 8:

Joseph had a full, one-litre bottle of water. He drank 320 millilitres of it. How much was left?

(A) 660 mL (B) 670 mL (C) 680 mL (D) 730 mL (E) 780 mL

Problem 9:

Which of these rectangles has an area of 24 square centimetres?



(A) Q only (B) Q and R only (C) R only (D) S only (E) P, Q, R and S

Problem 10:

This table shows Jai's morning routine. If he needs to be at school by $8: 55 \mathrm{am}$ what is the latest time he can start his shower?


(A) 7:35 am (B) 7: 50 am (C) 8:05 am (D) 8:20 am (E) 8:35 am

Problem 11:

Which spinner is twice as likely to land on red as white?

Problem 12:

Starting at 0 on the number line, Clement walks back and forth in the following pattern: 3 to the right, 2 to the left, 3 to the right, 2 to the left, and so on.

How many times does he walk past the position represented by $4 \frac{1}{2}$ ?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 13:

Three digits are missing from this sum. Toby worked out the missing numbers and added them together. What was his answer?

(A) 11 (B) 13 (C) 15 (D) 17 (E) 19

Problem 14:

I have three cardboard shapes: a square, a circle and a triangle. I glue them on top of each other as shown in this diagram.

I then flip the glued-together shapes over. What could they look like?

Problem 15:

What is the missing number needed to make this number sentence true? $270 \div 45=\square \div 15$

(A) 3 (B) 6 (C) 60 (D) 90 (E) 150

Problem 16:

Three different squares are arranged as shown. The perimeter of the largest square is 32 centimetres. The area of the smallest square is 9 square centimetres. What is the perimeter of the mediumsized square?

(A) 12 cm (B) 14 cm (C) 20 cm (D) 24 cm (E) 30 cm

Problem 17:

Huang has a bag of marbles. Mei takes out one-third of them. Huang then takes out one-half of those left, leaving 8 marbles in the bag. How many marbles were originally in the bag?

(A) 12 (B) 16 (C) 18 (D) 24 (E) 36

Problem 18:

A different positive whole number is placed at each vertex of a cube. No two numbers joined by an edge of the cube can have a difference of 1.

What is the smallest possible sum of the eight numbers?

(A) 36 (B) 37 (C) 38 (D) 39 (E) 40

Problem 19:

George is 78 this year. He has three grandchildren: Michaela, Tom and Lucy. Michaela is 27 , Tom is 23 and Lucy is 16 . After how many years will George's age be equal to the sum of his grandchildren's ages?

(A) 3 (B) 6 (C) 9 (D) 10 (E) 12

Problem 20:

Ms Graham asked each student in her Year 5 class how many television sets they each have This graph shows the results.

How many television sets do the students have altogether?

(A) 9 (B) 29 (C) 91 (D) 99 (E) 101

Problem 21:

In a mathematics competition, 70 boys and 80 girls competed. Prizes were won by 6 boys and $15 \%$ of the girls. What percentage of the students were prize winners?

(A) $10 \%$ (B) $12 \%$ (C) $15 \%$ (D) $18 \%$ (E) $20 \%$

Problem 22:

Ariel writes the letters of the alphabet on a piece of paper as shown She turns the page upside down and looks at it in her bathroom mirror. How many of the letters appear unchanged when viewed this way?

(A) 0 (B) 3 (C) 4 (D) 6 (E) 9

Problem 23:

The Australian Mathematical College (AMC) has 1000 students. Each student takes 6 classes a day. Each teacher teaches 5 classes per day with 25 students in each class. How many teachers are there at the AMC?

(A) 40 (B) 48 (C) 50 (D) 200 (E) 240

Problem 24:

This list pqrs, pqsr, prqs, prsq, … can be continued to include all 24 possible arrangements of the four letters $p, q, r$ and $s$. The arrangements are listed in alphabetical order. Which one of the following is 19th in this list?

(A) $s p q r$ (B) $s r p q$ (C) $q p s r$ (D) $q r p s$ (E) $r p s q$

Problem 25:

In this puzzle, each circle should contain an integer. Each of the five lines of four circles should add to 40. When the puzzle is completed, what is the largest number used?

(A) 15 (B) 16 (C) 17 (D) 18 (E) 19

Problem 26:

Nguyen writes down some numbers according to the following rules. Starting with the number 1, he doubles the number and adds 4 , so the second number he writes is 6 . He now repeats this process, starting with the last number written, doubling and then adding 4, but he doesn't write the hundreds digit if the number is bigger than 100 . What is the 2022nd number that Nguyen writes down?

Problem 27:

Karen's mother made a cake for her birthday. After it was iced on the top and the 4 vertical faces, it was a cube with 20 cm sides. Darren was asked to decorate the cake with chocolate drops. He arranged them all over the icing in a square grid pattern, spaced with centres 2 cm apart. Those near the edges of the cube had centres 2 cm from the edge. The diagram shows one corner of the cake.

How many chocolate drops did Darren use to decorate Karen's cake?

Problem 28:

I choose three different numbers out of this list and add them together:

$$
1,3,5,7,9, \ldots, 105
$$

How many different totals can I get?

Problem 29:

The Athletics clubs of Albury and Wodonga agree to send a combined team to the regional championships. They have 11 sprinters on the combined team, 5 from Albury and 6 from Wodonga. For the $4 \times 100$ metre relay, they agree to have a relay team with two sprinters from the Albury club and two sprinters from the Wodonga club. How many relay teams are possible?

Problem 30:

The following is a net of a rectangular prism with some dimensions, in centimetres, given.

What is the volume of the rectangular prism in cubic centimetres?

Australian Mathematics Competition - 2023 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

This shape is made from 7 squares, each 1 cm by 1 cm . What is its perimeter?

(A) 7 cm (B) 12 cm (C) 14 cm (D) 16 cm (E) 28 cm

Problem 2:

There are five shapes here. How many are quadrilaterals?


(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 3:

In a board game, Nik rolls three standard dice, one at a time. He needs his three rolls to add to 12 . His first two dice rolls are 5 and 3 . What does he need his third roll to be?

(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

Problem 4:

In this diagram, how many of the small squares need to be shaded for the large rectangle to be one-quarter shaded?

(A) 2 (B) 3 (C) 4 (D) 6 (E) 12

Problem 5:

Petra left for school at 8:51 am. She got to school at 9:09 am. How long did it take Petra to get to school?

(A) 9 minutes (B) 10 minutes (C) 18 minutes (D) 42 minutes (E) 1 hour

Problem 6:

Which letter marks where 25 is on this number line?

Problem 7:

This bottle holds 4 glasses of water.

Which one of the following holds the most water?

Problem 8:

Two pizzas are shared equally between 3 students. What fraction of a whole pizza does each student get?

(A) $\frac{1}{2}$ (B) $\frac{1}{3}$ (C) $\frac{1}{4}$ (D) $\frac{2}{3}$ (E) $\frac{3}{4}$

Problem 9:

A piece of card is cut out and labelled as shown in the diagram.

It is folded along the dotted lines to make a box without a top. Which letter is on the bottom of the box?

(A) A (B) B (C) C (D) D (E) E

Problem 10:

Doughnuts come in bags of 3 and boxes of 8 . I bought exactly 25 doughnuts for my party.What do I get when I add the number of boxes I bought and the number of bags I bought?


(A) 4 (B) 5 (C) 6 (D) 7 (E) 8

Problem 11:

This line graph shows the temperature each hour during a day.

Roughly for how long was the temperature above $20^{\circ} \mathrm{C}$ ?

(A) 7 hours (B) 8 hours (C) 9 hours (D) 10 hours (E) 11 hours

Problem 12:

VIV takes her three children, HANNAH, OTTO and IZZI, out shopping. Each is wearing a t-shirt with their name on the front in capital letters. When they stand in front of the shop mirror, which names appear the same in the reflection as on the shirts?


(A) VIV and OTTO (B) VIV, OTTO and IZZI (C) VIV, HANNAH and IZZI (D) HANNAH and OTTO (E) All four of them

Problem 13:

This regular hexagon has angles of $120^{\circ}$ and the square has angles of $90^{\circ}$.

What is the angle $x^{\circ}$ in the diagram?

(A) $90^{\circ}$ (B) $120^{\circ}$ (C) $135^{\circ}$ (D) $150^{\circ}$ (E) $180^{\circ}$

Problem 14:

Syed's mother had some money to share with her family. She gave one-quarter of her money to Syed. Then she gave one-third of what was left to Ahmed. Then she gave one-half of what was left to Raiyan. She was left with $\$ 15$, which she kept for herself. How much money did Syed's mother have to start with?

(A) $\$ 30$ (B) $\$ 45$ (C) $\$ 60$ (D) $\$ 90$ (E) $\$ 120$

Problem 15:

The rectangle shown has a side length of 9 cm . It is divided into 3 identical rectangles as shown. What is the area, in square centimetres, of the original rectangle?

(A) 45 (B) 50 (C) 52 (D) 54 (E) 63

Problem 16:

This diagram shows a rectangle with a perimeter of 30 cm . It has been divided by 2 lines into 4 small rectangles. Three of the small rectangles have the perimeters shown. What is the perimeter of fourth small rectangle?

(A) 10 cm (B) 12 cm (C) 14 cm (D) 16 cm (E) 18 cm

Problem 17:

There are 10 questions in a test. Each correct answer scores 5 points, each wrong answer loses 3 points, and if a question is left blank it scores 0 points. Tycho did this test and scored 27 points. How many questions did Tycho leave blank?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 18:

Estelle is making decorations shaped like the 8-pointed star shown. She folds a square of paper to make a triangle with 8 layers as shown.

How could she cut the triangle so that the unfolded shape is the star?

Problem 19:

Earlier this year Ben said, 'Next year I will turn 13 , but 2 days ago I was $10 . '$ Ben's birthday is

(A) 1st January (B) 2nd January (C) 29th December (D) 30th December (E) 31st December

Problem 20:

Peyton, Luka and Dan have 180 stickers in total. Peyton has half as many stickers as Luka. Dan has three times as many as Luka.
How many stickers does Peyton have?

(A) 20 (B) 24 (C) 30 (D) 40 (E) 54

Problem 21:

Mrs Graaf invents a game for her students to practise arithmetic. They roll two 10 -sided dice to pick two random numbers. Starting at one of the numbers, they keep adding the other number until they reach a 3-digit number. Ian rolls a 5 and an 8 . If he chooses to start with 5 and then add 8 again and again, his list is $5,13,21, \ldots$, 93,101 . If he chooses to start with 8 and add 5 , his list is $8,13,18, \ldots, 98,103$ On Nara's turn, she makes a list that ends with 107. What pair of numbers could she have rolled?

(A) 4 and 8 (B) 5 and 7 (C) 3 and 4 (D) 6 and 9 (E) 3 and 8

Problem 22:

At a school concert, the tickets cost $\$ 20$ per adult and $\$ 2$ per child. The total paid by the 100 people who attended was $\$ 920$. How many were children?

(A) between 25 and 35 (B) between 35 and 45 (C) between 45 and 55 (D) between 55 and 65 (E) between 65 and 75

Problem 23:

Meena has a standard dice, with each pair of opposite faces adding to 7 . At first, the three faces she can see add to 6 , as shown. She holds the dice between a pair of opposite faces and rotates it $180^{\circ}$, keeping these opposite faces facing the same direction. She puts the dice back down and adds up the three faces she can now see.

What is the smallest possible total she could get?

(A) 6 (B) 8 (C) 10 (D) 12 (E) 14

Problem 24:

I have 4 whole numbers that add up to 98. If I were to add 6 to the first number, subtract 6 from the second number, multiply the third number by 6 and divide the fourth number by 6, the four answers would all be the same. What is the sum of the largest two of my original four numbers?

(A) 72 (B) 86 (C) 88 (D) 90 (E) 94

Problem 25:

When I ride my bike at 20 kilometres per hour, each wheel turns at 2 revolutions per second. When I ride 1 kilometre, how many revolutions does each wheel make?

(A) 40 (B) 240 (C) 320 (D) 360 (E) 420

Problem 26:

Problem 27:

Li attempted to multiply a single-digit number by 36 , but he accidentally multiplied by 63 instead. His answer was 189 larger than the correct answer. What was the correct answer to the multiplication?

Problem 28:

Using 9 out of the 10 possible digits Safia writes 3 numbers, each between 100 and 999. She adds her 3 numbers together. What is the smallest possible sum?

Problem 29:

Yifan has a construction set consisting of red, blue and yellow rods. All rods of the same colour are the same length, but differently coloured rods are different lengths. She wants to make quadrilaterals using these rods.

What number do you get when you multiply the lengths of one red rod, one blue rod and one yellow rod?

Problem 30:

Janus is making patterns using square tiles. Each pattern is made by copying the previous pattern, then adding a tile to every grid square that shares an edge with the copied pattern.

His last pattern is the largest one that can be made with fewer than 1000 tiles. How many tiles are in this last pattern?

Counting Chains with Casework in Combinatorics: A Problem from the RMO 2024

In this exploration, we dive into a combinatorial problem from the 2024 Regional Math Olympiad (RMO) in India, centered on counting specific number sequences, called "chains." Using a function \ (f(n) \), defined as the number of chains that start at 1 and end at \( n \) with each previous number dividing the next, the problem applies strategic casework to calculate \( f(2^m \cdot 3) \).

See the Question

Problem Overview

We want to determine:
\(f(2^m \cdot 3)\)
where each chain is a sequence that:

  1. Begins at 1 and ends at \( 2^m \cdot 3 \),
  2. Has each term dividing the next.

Concepts Used:

  1. Combinatorial Casework: Breaking down problems by considering specific scenarios helps in counting complex structures systematically.
  2. Binomial Theorem: Key in calculating possible combinations, where the sum of binomial coefficients up to \( n \) equals \( 2^n \).

Watch the Video

Solution Outline:

The solution involves structured casework using the position of the first appearance of 3 as a "switch" to organize sub-cases.

Understanding Chains

Casework on Position of 3:

Applying Binomial Coefficients:

Final Answer:

By organizing cases and summing possibilities, we obtain the final count:
\[2^{m-1} \cdot (m + 2)\]

This problem exemplifies the effectiveness of casework in combinatorics, teaching a methodical approach to counting sequences. Through strategic splitting and summing, it provides a beautiful solution to a challenging problem in combinatorial mathematics.

Singapore Math Olympiad Past years Questions- Combinatorics (Senior)

Problem 01: (Year 2023, Problem 22)

Find the number of possible ways of arranging \(m\) ones and \(n\) zeros in a row such that there are in total \(2 k+1\) strings of ones and zeros. For example, \(1110001001110001\) consists of 4 strings of ones and 3 strings of zeros.

Problem 02: (Year 2021, Problem 23)

The following \(3 \times 5\) rectangle consists of \(151 \times 1\) squares. Determine the number of ways in which 9 out of the 15 squares are to be coloured in black such that every row and every column has an odd number of black squares.

Problem 03: (Year 2020, Problem 23)

There are 6 couples, each comprising a husband and a wife. Find the number of ways to divide the 6 couples into 3 teams such that each team has exactly 4 members, and that the husband and the wife from the same couple are in different teams.

Problem 04: (Year 2019, Problem 22)

Eleven distinct chemicals \(C_1, C_2, \ldots, C_{11}\) are to be stored in three different warehouses. Each warehouse stores at least one chemical. A pair \(C_i, C_j\) of chemicals, where \(i \neq j\), is either compatible or incompatible. Any two incompatible chemicals cannot be stored in the same warehouse. However, a pair of compatible chemicals may or may not be stored in the same warehouse. Find the maximum possible number of pairs of incompatible chemicals that can be found among the stored chemicals.

Problem 05: (Year 2020, Problem 24)

Some students sat for a test. The first group of students scored an average of 91 marks and were given Grade A. The second group of students scored an average of 80 marks and were given Grade B. The last group of students scored an average of 70 marks and were given Grade \(\mathrm{C}\). The numbers of students in all three groups are prime numbers and the total score of all the students is 1785 . Determine the total number of students.

Singapore Math Olympiad Past ears Questions- Combinatorics (Junior)

Problem 04 - SMO Year 2022

A shop sells two types of buns, with either cream or jam filling, which are indistinguishable until someone bites into the buns. Four mathematicians visited the shop and ordered (not necessarily in that sequence): three cream buns, two cream buns and one jam bun, one cream and two jam buns, and three jam buns. Each knew precisely what the others had ordered. Unfortunately, the shop owner mixed up the orders and gave each mathematician the wrong order!
The mathematicians started eating, all still unaware of the mixup, until the shop owner ran over to inform them of the mistake. Mathematician A said: "I ate two buns and both had cream filling. So, if my order was wrong, I now know what type my third bun is." Mathematician B then said: "I only ate one bun and it had cream filling. Based on what A said and since I remember A's order, I now know what type my other two buns are." Finally, Mathematician C said: "I have not started eating but I must have received three jam buns." Which of the following statements about Mathematician D is correct?


(A) D ordered two cream and one jam but received three jam buns.
(B) D ordered one cream and two jam but received two cream and one jam buns.
(C) D ordered three cream but received one cream and two jam buns.
(D) D ordered three jam but received three cream buns.
(E) None of the above

Problem 07- SMO Year 2022

The digits (1,2,3,4,5) and 6 are arranged to form two positive integers with each digit appearing exactly once. How many ways can this be done if the sum of the two integers is 570 ?

Problem 13 - SMO Year 2022

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(\mathrm{W}\) represents 5 , what number does TROOP represent?

Problem 16 - SMO Year 2022

Eggs in a certain supermarket are sold only in trays containing exactly 10,12 or 30 eggs per tray. It is thus impossible to buy exactly 14 eggs or any odd number of eggs. However, it is possible to buy exactly 78 eggs using four trays of 12 and one tray of 30 . What is the largest even number of eggs that is impossible to be bought from this supermarket?

Problem 11 - SMO Year 2021:

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(S\) represents \(6 \)and \(E\) represents \(8\),-what number does SIX represent?

Problem 21 - SMO Year 2021

In chess, two queens are said to be attacking each other if they are positioned in the same row, column or diagonal on a chessboard. How many ways are there to place two identical queens in a (4 \times 4) chessboard such that they do not attack each other?
\(\frac{1}{2} \times \frac{1}{4} \times 401 \times 403 x \times 801=\)

Problem 23 - SMO Year 2021:

A \(3 \times 3\) grid is filled with the integers 1 to 9 . An arrangement is nicely ordered if the integers in each horizontal row is increasing from left to right and the integers in each vertical column is increasing from top to bottom. Two examples of nicely ordered arrangements are given in the diagram below. What is the total number of distinct nicely ordered arrangements?

Problem 24 - SMO Year 2021:

A class has exactly 50 students and it is known that 40 students scored (A) in English, 45 scored (A) in Mathematics and 42 scored (A) in Science. What is the minimum number students who scored (A) in all three subjects?

Problem 02 - SMO Year 2020:

An expensive painting was stolen and the police rounded up five suspects Alfred, Boris, Chucky, Dan and Eddie. These were the statements that were recorded.
Alfred: "Either Boris or Dan stole the painting."
Boris: "I think Dan or Eddie is the guilty party."
Chucky: "It must be Dan."
Dan: "Boris or Eddie did it!"
Eddie: "I am absolutely sure the thief is Alfred."
The police knew that only one of the five suspects stole the painting and that all five were lying. Who stole the painting?
(A) Alfred
(B) Boris
(C) Chucky
(D) Dan
(E) Eddie

Problem 12 - SMO Year 2020:

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If the letter K represents 6 , what number does SHAKE represent?

Problem 21- SMO Year 2020:

Ali and Barry went running on a standard 400 metre track. They started simultaneously at the same location on the track but ran in opposite directions. Coincidentally, after 24 minutes, they ended at the same location where they started. Ali completed 12 rounds of the track in those 24 minutes while Barry completed 10 rounds. How many times did Ali and Barry pass each other during the run? (Exclude from your answer the times that they met at the start of the of run and when they completed the run after 24 minutes.)

Problem 2 - SMO Year 2019

In a strange island. there are only two types of inhabitants: truth-tellers who only tell the truth and liars who only tell lies. One day, you meet two such inhabitants \(A\) and \(B\). \(A\) said "Exactly one of us is a truth teller." \(B\) kept silent. Which of the following must be true?

(A) Both \(A\) and \(B\) are truth-tellers
(B) Both \(A\) and \(B\) are liars
(C) \(A\) is a truth-teller and \(B\) is a liar
(D) \(A\) is a liar and \(B\) is a truth-teller
(E) Not enough information to decide

Problem 19 - SMO Year 2019

In the figure below, each distinct letter represents a unique digit such that the arithmetic holds. What digit does the letter \(\mathrm{L}\) represent?

Problem 22 - SMo Year 2019

Two secondary one and \(m\) secondary two students took part in a round-robin chess tournament. In other words, each student played with every other student exactly once. For each match, the winner receives 3 points and the loser 0 points. If a match ends in a draw, both contestants receive 1 point each. If the total number of points received by all students was 130 , and the number of matches that ended in a draw was less than half of the total number of matches played, what is the value of \(m\) ?