Problem 1

What is the value of $9901 \cdot 101-99 \cdot 10101 ?$

(A) 2
(B) 20
(C) 200
(D) 202
(E) 2020

Problem 2

A model used to estimate the time it will take to hike to the top of the mountain on a trail is of the form $T=a L+b G$, where $a$ and $b$ are constants, $T$ is the time in minutes, $L$ is the length of the trail in miles, and $G$ is the altitude gain in feet. The model estimates that it will take 69 minutes to hike to the top if a trail is 1.5 miles long and ascends 800 feet, as well as if a trail is 1.2 miles long and ascends 1100 feet. How many minutes does the model estimates it will take to hike to the top if the trail is 4.2 miles long and ascends 4000 feet?

(A) 240
(B) 246
(C) 252
(D) 258
(E) 264

Problem 3

What is the sum of the digits of the smallest prime that can be written as a sum of 5 distinct primes?

(A) 5
(B) 7
(C) 9
(D) 10
(E) 13

Problem 4

The number 2024 is written as the sum of not necessarily distinct two-digit numbers. What is the least number of two-digit numbers needed to write this sum?

(A) 20
(B) 21
(C) 22
(D) 23
(E) 24

Problem 5

What is the least value of $n$ such that $n$ ! is a multiple of 2024 ?

(A) 11
(B) 21
(C) 22
(D) 23
(E) 253

Problem 6

What is the minimum number of successive swaps of adjacent letters in the string $A B C D E F$ that are needed to change the string to $F E D C B A$ ? (For example, 3 swaps are required to change $A B C$ to $C B A$; one such sequence of swaps is $
A B C \rightarrow B A C \rightarrow B C A \rightarrow C B A .)$

(A) 6
(B) 10
(C) 12
(D) 15
(E) 24

Problem 7

The product of three integers is 60. What is the least possible positive sum of the three integers?

(A) 2
(B) 3
(C) 5
(D) 6
(E) 13

Problem 8

Amy, Bomani, Charlie, and Daria work in a chocolate factory. On Monday Amy, Bomani, and Charlie started working at $1: 00 P M$ and were able to pack 4,3 , and 3 packages, respectively, every 3 minutes. At some later time, Daria joined the group, and Daria was able to pack 5 packages every 4 minutes. Together, they finished packing 450 packages at exactly $2: 45 P M$. At what time did Daria join the group?

(A) $1: 25 \mathrm{PM}$
(B) $1: 35 \mathrm{PM}$
(C) $1: 45 \mathrm{PM}$
(D) 1:55 PM
(E) 2:05 PM

Problem 9

In how many ways can 6 juniors and 6 seniors form 3 disjoint teams of 4 people so that each team has 2 juniors and 2 seniors?

(A) 720
(B) 1350
(C) 2700
(D) 3280
(E) 8100

Problem 10

Consider the following operation. Given a positive integer $n$, if $n$ is a multiple of 3 , then you replace $n$ by $\frac{n}{3}$. If $n$ is not a multiple of 3 , then you replace $n$ by $n+10$. Then continue this process. For example, beginning with $n=4$, this procedure gives $4 \rightarrow 14 \rightarrow 24 \rightarrow 8 \rightarrow 18 \rightarrow 6 \rightarrow$

$ 2 \rightarrow 12 \rightarrow \cdots$. Suppose you start with $n=100$. What value results if you perform this operation exactly 100 times?

(A) 10
(B) 20
(C) 30
(D) 40
(E) 50

Problem 11

How many ordered pairs of integers $(m, n)$ satisfy $\sqrt{n^2-49}=m$ ?

(A) 1
(B) 2
(C) 3
(D) 4
(E) Infinitely many

Problem 12

Zelda played the Adventures of Math game on August 1 and scored 1700 points. She continued to play daily over the next 5 days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was $1700+80=1780$ points.) What was Zelda's average score in points over the 6 days?

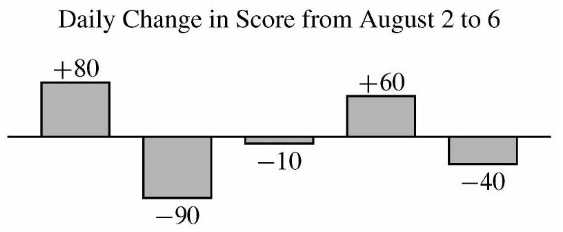
(A) 1700
(B) 1702
(C) 1703
(D) 1713
(E) 1715

Problem 13

Two transformations are said to commute if applying the first followed by the second gives the same result as applying the second followed by the first. Consider these four transformations of the coordinate plane:

• a translation 2 units to the right,
• a $90^{\circ}$-rotation counterclockwise about the origin,
• a reflection across the $x$-axis, and
• a dilation centered at the origin with scale factor 2.

Of the 6 pairs of distinct transformations from this list, how many commute?

(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 14

One side of an equilateral triangle of height 24 lies on line $\ell$. A circle of radius 12 is tangent to line $l$ and is externally tangent to the triangle. The area of the region exterior to the triangle and the circle and bounded by the triangle, the circle, and line $\ell$ can be written as $a \sqrt{b}-c \pi$, where $a$, $b$, and $c$ are positive integers and $b$ is not divisible by the square of any prime. What is $a+b+c$ ?

(A) 72
(B) 73
(C) 74
(D) 75
(E) 76

Problem 15

Let $M$ be the greatest integer such that both $M+1213$ and $M+3773$ are perfect squares. What is the units digit of $M$ ?

(A) 1
(B) 2
(C) 3
(D) 6
(E) 8

Problem 16

All of the rectangles in the figure below, which is drawn to scale, are similar to the enclosing rectangle. Each number represents the area of the rectangle. What is length $A B$ ?

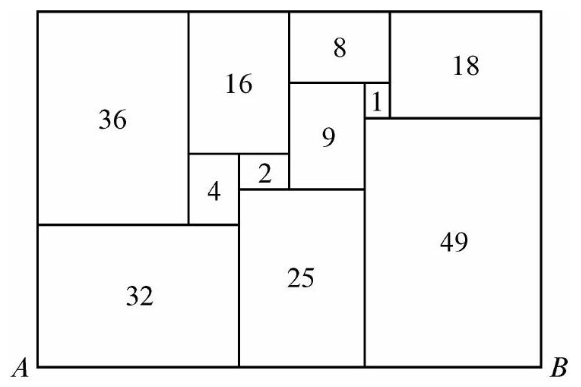
Problem 17

Two teams are in a best-two-out-of-three playoff: the teams will play at most 3 games, and the winner of the playoff is the first team to win 2 games. The first game is played on Team A's home field, and the remaining games are played on Team B's home field. Team A has a $\frac{2}{3}$ chance of winning at home, and its probability of winning when playing away from home is $p$. Outcomes of the games are independent. The probability that Team A wins the playoff is $\frac{1}{2}$. Then $p$ can be written in the form $\frac{1}{2}(m-\sqrt{n})$, where $m$ and $n$ are positive integers. What is $m+n$ ?

(A) 10
(B) 11
(C) 12
(D) 13
(E) 14

Problem 18

There are exactly $K$ positive integers $b$ with $5 \leq b \leq 2024$ such that the base- $b$ integer $2024_b$ is divisible by 16 (where 16 is in base ten). What is the sum of the digits of $K$ ?

(A) 16
(B) 17
(C) 18
(D) 20
(E) 21

Problem 19

The first three terms of a geometric sequence are the integers $a, 720$, and $b$, where $a<720<b$. What is the sum of the digits of the least possible value of $b$ ?

(A) 9
(B) 12
(C) 16
(D) 18
(E) 21

Problem 20

Let $S$ be a subset of ${1,2,3, \ldots, 2024}$ such that the following two conditions hold:

• If $x$ and $y$ are distinct elements of $S$, then $|x-y|>2$
• If $x$ and $y$ are distinct odd elements of $S$, then $|x-y|>6$.

What is the maximum possible number of elements in $S$ ?

(A) 436
(B) 506
(C) 608
(D) 654
(E) 675

Problem 21

The numbers, in order, of each row and the numbers, in order, of each column of a $5 \times 5$ array of integers form an arithmetic progression of length 5 . The numbers in positions $(5,5),(2,4),(4,3)$, and $(3,1)$ are $0,48,16$, and 12 , respectively. What number is in position $(1,2) ?$

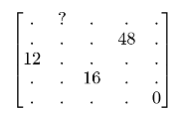
(A) 19
(B) 24
(C) 29
(D) 34
(E) 39

Problem 22

Let $\mathcal{K}$ be the kite formed by joining two right triangles with legs 1 and $\sqrt{3}$ along a common hypotenuse. Eight copies of $\mathcal{K}$ are used to form the polygon shown below. What is the area of triangle $\triangle A B C$ ?

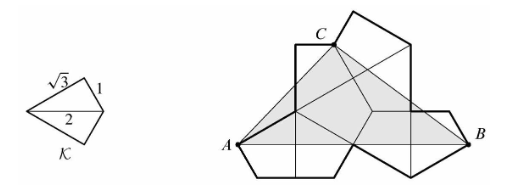
(A) $2+3 \sqrt{3}$
(B) $\frac{9}{2} \sqrt{3}$
(C) $\frac{10+8 \sqrt{3}}{3}$
(D) 8
(E) $5 \sqrt{3}$

Problem 23

Integers $a, b$, and $c$ satisfy $a b+c=100, b c+a=87$, and $c a+b=60$. What is $a b+b c+c a$ ?

(A) 212
(B) 247
(C) 258
(D) 276
(E) 284

Problem 24

A bee is moving in three-dimensional space. A fair six-sided die with faces labeled $A^{+}, A^{-}, B^{+}, B^{-}, C^{+}$, and $C^{-}$is rolled. Suppose the bee occupies the point $(a, b, c)$. If the die shows $A^{+}$, then the bee moves to the point $(a+1, b, c)$ and if the die shows $A^{-}$, then the bee moves to the point $(a-1, b, c)$. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point $(0,0,0)$ and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?

(A) $\frac{1}{54}$
(B) $\frac{7}{54}$
(C) $\frac{1}{6}$
(D) $\frac{5}{18}$
(E) $\frac{2}{5}$

Problem 25

The figure below shows a dotted grid 8 cells wide and 3 cells tall consisting of $1^{\prime \prime} \times 1^{\prime \prime}$ squares. Carl places 1 -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?

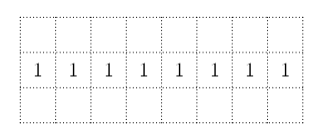
(A) 130
(B) 144
(C) 146
(D) 162
(E) 196